【题目】如图,A是半径为12cm的⊙O上的定点,动点P从A出发,以2πcm/s的速度沿圆周逆时针运动,当点P回到点A立即停止运动.
(1)如果∠POA=90°,求点P运动的时间;
(2)如果点B是OA延长线上的一点,AB=OA,那么当点P运动的时间为2s时,判断直线BP与⊙O的位置关系,并说明理由.

参考答案:
【答案】(1)点P运动的时间为3s或9s;(2)直线BP与⊙O相切,理由见解析.
【解析】
(1)当∠POA=90°时,点P运动的路程为⊙O周长的![]() 或
或![]() ,所以分两种情况进行分析即可得;
,所以分两种情况进行分析即可得;
(2)直线BP与⊙O的位置关系是相切,根据已知可证得OP⊥BP,即直线BP与⊙O相切.
(1)当∠POA=90°时,根据弧长公式可知点P运动的路程为⊙O周长的![]() 或
或![]() ,
,
设点P运动的时间为ts,
当点P运动的路程为⊙O周长的![]() 时,2πt=
时,2πt=![]() 2π12,解得t=3;
2π12,解得t=3;
当点P运动的路程为⊙O周长的![]() 时,2πt=
时,2πt=![]() 2π12,解得t=9,
2π12,解得t=9,
∴当∠POA=90°时,点P运动的时间为3s或9s;
(2)如图,当点P运动的时间为2s时,直线BP与⊙O相切.理由如下:
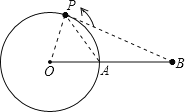
当点P运动的时间为2s时,点P运动的路程为4πcm,连接OP,PA,
∵半径AO=12,∴⊙O的周长为24π,
∴![]() 的长为⊙O周长的
的长为⊙O周长的![]() ,∴∠POA=60°,
,∴∠POA=60°,
∵OP=OA,∴△OAP是等边三角形,
∴OP=OA=AP,∠OAP=60°,
∵AB=OA,∴AP=AB,
∵∠OAP=∠APB+∠B,∴∠APB=∠B=30°,
∴∠OPB=∠OPA+∠APB=90°,
∴OP⊥BP,∴直线BP与⊙O相切.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,△ABC内接于⊙O,AB=8,AC=4,D是AB边上一点,P是优弧
 的中点,连接PA,PB,PC,PD,当BD的长度为多少时,△PAD是以AD为底边的等腰三角形?并加以证明.
的中点,连接PA,PB,PC,PD,当BD的长度为多少时,△PAD是以AD为底边的等腰三角形?并加以证明.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,△ABC中,∠ACB=90°,∠B=30°,AD平分∠CAB,延长AC至E,使CE=AC.
(1)求证:DE=DB;
(2)连接BE,试判断△ABE的形状,并说明理由.

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,半径为R的圆内,ABCDEF是正六边形,EFGH是正方形.
(1)求正六边形与正方形的面积比;(2)连接OF,OG,求∠OGF.

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图①,点
 ,
, ,
, ,
, 在一条直线上,
在一条直线上, ,过
,过 ,
, 分别作
分别作 ,
,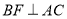 ,若
,若 .
.
(1)求证:
 .
.(2)若将
 的边
的边 沿
沿 方向移动得到图②,其他条件不变,(1)中结论是否仍然成立?请说明理由.
方向移动得到图②,其他条件不变,(1)中结论是否仍然成立?请说明理由. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在△ABC中,AB=5,AC=3,BC=4,将△ABC绕A逆时针方向旋转40°得到△ADE,点B经过的路径为弧BD,是图中阴影部分的面积为( )

A.
 π﹣6 B.
π﹣6 B.  π C.
π C. 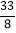 π﹣3 D.
π﹣3 D.  +π
+π -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在△ACB中,∠ACB=90°,AC=BC,点C的坐标为(﹣2,0),点A的坐标为(﹣6,3),求点B的坐标.

相关试题

