【题目】已知:如图,△ABC中,BO,CO分别是∠ABC和∠ACB的平分线,过O点的直线分别交AB、AC于点D、E,且DE∥BC.若AB=6cm,AC=8cm,则△ADE的周长为__.

参考答案:
【答案】14cm.
【解析】两直线平行,内错角相等,以及根据角平分线性质,可得△OBD、△EOC均为等腰三角形,由此把△AEF的周长转化为AC+AB.
解:∵DE∥BC,∴∠DOB=∠OBC,又∵BO是∠ABC的角平分线,∴∠DBO=∠OBC,∴∠DBO=∠DOB,∴BD=OD,同理:OE=EC,
∴△ADE的周长=AD+OD+OE+EC=AD+BD+AE+EC=AB+AC=14cm.
答案是:14cm.
“点睛”本题考查了平行线的性质和等腰三角形的判定及性质,正确证明△OBD、△EOC均为等腰三角形是关键.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,是用围棋子摆出的图案(用棋子的位置用用有序数对表示,如A点在(5,1)),如果再摆一黑一白两枚棋子,使9枚棋子组成的图案既是轴对称图形又是中心对称图形,则下列摆放正确的是( )

A. 黑(3,3),白(3,1) B. 黑(3,1),白(3,3)
C. 黑(1,5),白(5,5) D. 黑(3,2),白(3,3)
-
科目: 来源: 题型:
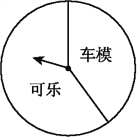
查看答案和解析>>【题目】某商场“六一”期间进行一个有奖销售的活动,设立了一个可以自由转动的转盘(如图),并规定:顾客购物100元以上就能获得一次转动转盘的机会,当转盘停止时,指针落在哪一区域就可以获得相应的奖品(若指针落在两个区域的交界处,则重新转动转盘).下表是此次促销活动中的一组统计数据:
转动转盘的次数n
100
200
400
500
800
1 000
落在“可乐”区域
的次数m
60
122
240
298
604
落在“可乐”
区域的频率
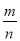
0.6
0.61
0.6
0.59
0.604
(1)计算并完成上述表格;
(2)请估计当n很大时,频率将会接近__________;假如你去转动该转盘一次,你获得“可乐”的概率约是__________;(结果精确到0.1)
(3)在该转盘中,表示“车模”区域的扇形的圆心角约是多少度?
-
科目: 来源: 题型:
查看答案和解析>>【题目】下列计算正确的是( )
A.﹣3a+4a=﹣7a
B.4m+2n=6mn
C.5x+4x=20x2
D.6xy3﹣2xy3=4xy3 -
科目: 来源: 题型:
查看答案和解析>>【题目】下列运算正确的是( )
A.3a2﹣2a2=1
B.(a2)3=a5
C.a2a4=a6
D.(3a)2=6a2 -
科目: 来源: 题型:
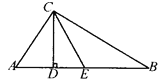
查看答案和解析>>【题目】已知:如图,在△ABC中,∠ACB=90°,CD为高,CE平分∠BCD,且∠ACD:∠BCD=1:2,那么CE是AB边上的中线对吗?说明理由.
-
科目: 来源: 题型:
查看答案和解析>>【题目】下列不等式中,解集不同的是( ).
A. 5x>10与3x>6 B. 6x-9<3x+6 与x<5
C. x<-2与-14x>28 D. x-7<2x+8与x>15
相关试题

