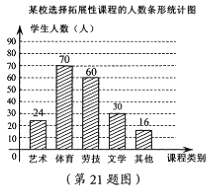
【题目】为深化义务教育课程改革,某校积极开展拓展性课程建设,设计开设艺术、体育、劳技、文学等多个类别的拓展性课程,要求每一位学生都自主选择一个类别的拓展性课程。为了了解学生选择拓展性课程的情况,随机抽取了部分学生进行调查,并将调查结果绘制成如下统计图(部分信息未给出):

根据统计图中的信息,解答下列问题:
(1)求本次被调查的学生人数;
(2)将条形图补充完整;
(3)若该校共有1600名学生,请估计全校选择体育类的学生人数。
参考答案:
【答案】(1)200人;(2)详见解析;(3)560人.
【解析】
试题分析:(1)用选择劳技拓展性课程的学生人数除以选择劳技拓展性课程的学生人数所占的百分比即可得本次被调查的学生人数;(2)先求得选择文学拓展性课程的学生人数和选择体育拓展性课程的学生人数,再补全条形图即可;(3)用总人数乘以选择体育拓展性课程的学生的人数所占的百分比即可.
试题解析:(1)60÷30%=200(人);
(2)200×15%=30(人)
200-24-60-30-16=70(人)
补全条形图如下:
 ;
;
(3)1600×![]() =560(人)
=560(人)
答:估计全校选择体育类的学生有560人.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,有一块铁皮,拱形边缘呈抛物线状,MN=4,抛物线顶点处到边MN的距离是4,要在铁皮上截下一矩形ABCD,使矩形顶点B、C落在边MN上,A、D落在抛物线上.
(1)如图建立适当的坐标系,求抛物线解析式;
(2)设矩形ABCD的周长为L,点C的坐标为(m,0),求L与m的关系式(不要求写自变量取值范围).
(3)问这样截下去的矩形铁皮的周长能否等于9.5,若不等于9.5,请说明理由,若等于9.5,求出吗的值?

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,一次函数y1=kx+b的图象与反比例函数
 的图象交于A(﹣2,1),B(1,n)两点.
的图象交于A(﹣2,1),B(1,n)两点.(1)试确定上述反比例函数和一次函数的表达式.
(2)求△AOB的面积.
(3)比较y1和y2的大小.

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在矩形ABCD中,AB=3,BC=2,点E为AD中点,点F为BC边上任一点,过点F分别作EB,EC的垂线,垂足分别为点G,H,则FG+FH为( ).

A.
 B.
B.
 C.
C.
 D.
D.

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,一棵大树在一次强台风中折断倒下,未折断树杆
 与地面仍保持垂直的关系,而折断部分
与地面仍保持垂直的关系,而折断部分 与未折断树杆
与未折断树杆 形成
形成 的夹角.树杆
的夹角.树杆 旁有一座与地面垂直的铁塔
旁有一座与地面垂直的铁塔 ,测得
,测得 米,塔高
米,塔高 米.在某一时刻的太阳照射下,未折断树杆
米.在某一时刻的太阳照射下,未折断树杆 落在地面的影子
落在地面的影子 长为
长为 米,且点
米,且点 、
、 、
、 、
、 在同一条直线上,点
在同一条直线上,点 、
、 、
、 也在同一条直线上.求这棵大树没有折断前的高度.(结果精确到
也在同一条直线上.求这棵大树没有折断前的高度.(结果精确到 ,参考数据:
,参考数据:  ,
,  ,
,  ).
).
-
科目: 来源: 题型:
查看答案和解析>>【题目】问题探究
(
 )如图①,已知正方形
)如图①,已知正方形 的边长为
的边长为 ,点
,点 和
和 分别是边
分别是边 、
、 上两点,且
上两点,且 .连接
.连接 和
和 ,交于点
,交于点 .猜想
.猜想 与
与 的位置关系,并证明你的结论.
的位置关系,并证明你的结论.(
 )如图②,已知正方形
)如图②,已知正方形 的边长为
的边长为 ,点
,点 和
和 分别从点
分别从点 、
、 同时出发,以相同的速度沿
同时出发,以相同的速度沿 、
、 方向向终点
方向向终点 和
和 运动,连接
运动,连接 和
和 ,交于点
,交于点 ,求
,求 周长的最大值.
周长的最大值.问题解决
(
 )如图③,
)如图③, 为边长为
为边长为 的菱形
的菱形 的对角线,
的对角线,  .点
.点 和
和 分别从点
分别从点 、
、 同时出发;以相同的速度沿
同时出发;以相同的速度沿 、
、 向终点
向终点 和
和 运动,连接
运动,连接 和
和 ,交于点
,交于点 ,求
,求 周长的最大值.
周长的最大值.


-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,
 是⊙
是⊙ 的直径,
的直径,  是⊙
是⊙ 的切线,
的切线,  为切点,
为切点,  交⊙
交⊙ 于点
于点 .
.(Ⅰ)若
 为
为 的中点,证明:
的中点,证明:  是⊙
是⊙ 的切线.
的切线.(Ⅱ)若
 ,
,  ,求
,求 的度数.
的度数.
相关试题

