【题目】设θ为直角三角形的一个锐角,给出θ角三角函数的两条基本性质:①tanθ=![]() ;②cos2θ+sin2θ=1,利用这些性质解答本题.已知cosθ+sinθ=
;②cos2θ+sin2θ=1,利用这些性质解答本题.已知cosθ+sinθ=![]() ,求值:
,求值:
(1)tanθ+![]() ; (2)|cosθ-sinθ|.
; (2)|cosθ-sinθ|.
参考答案:
【答案】(1)4;(2)![]() .
.
【解析】
(1)将tanθ=![]() 代入tanθ+
代入tanθ+![]() 并且通分发现
并且通分发现![]() ,求出cosθsinθ,代入计算即可;(2)先将所求的式子平方,展开后得到cos2θ﹣2cosθsinθ+sin2θ,再将第一步求解中的cosθsinθ=
,求出cosθsinθ,代入计算即可;(2)先将所求的式子平方,展开后得到cos2θ﹣2cosθsinθ+sin2θ,再将第一步求解中的cosθsinθ=![]() ,cos2θ+sin2θ=1代入计算,再求出算数平方根即可.
,cos2θ+sin2θ=1代入计算,再求出算数平方根即可.
(1)∵cosθ+sinθ=![]() ,
,
∴(cosθ+sinθ)2=(![]() )2,
)2,
cos2θ+2cosθsinθ+sin2θ=![]() ,
,
cosθsinθ=![]() ,
,
∴tanθ+![]()
=![]() +
+![]()
=![]()
=![]()
=4
(2)∵(cosθ﹣sinθ)2=cos2θ﹣2cosθsinθ+sin2θ=1﹣2×![]() =
=![]() ,
,
∴cosθ﹣sinθ=±![]() ,
,
∴|cosθ﹣sinθ|=![]() .
.
-
科目: 来源: 题型:
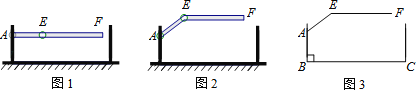
查看答案和解析>>【题目】某地下车库出口处安装了“两段式栏杆”,如图1所示,点A是栏杆转动的支点,点E是栏杆两段的联结点.当车辆经过时,栏杆AEF最多只能升起到如图2所示的位置,其示意图如图3所示(栏杆宽度忽略不计),其中AB⊥BC,EF∥BC,∠AEF=143°,AB=AE=1.2米,那么适合该地下车库的车辆限高标志牌为( )(参考数据:sin37°≈0.60,cos37°≈0.80,tan37°≈0.75)
A.
 B.
B. C.
C. D.
D.
-
科目: 来源: 题型:
查看答案和解析>>【题目】某测量队在山脚A处测得山上树顶仰角为45°(如图),测量队在山坡上前进600米到D处,再测得树顶的仰角为60°,已知这段山坡的坡角为30°,如果树高为15米,则山高为( )(精确到1米,
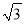 =1.732).
=1.732).
A. 585米 B. 1014米 C. 805米 D. 820米
-
科目: 来源: 题型:
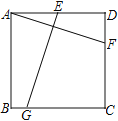
查看答案和解析>>【题目】如图,在边长为6的正方形ABCD中,点F为CD上一点,E是AD的中点,且DF=2.在BC上找点G,使EG=AF,则BG的长是___________
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在Rt△ABC中,∠C=90°,点D是BC边的中点,BD=2,tanB=
 .
.(1)求AD和AB的长;
(2)求sin∠BAD的值.

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,BC是路边坡角为30°,长为10米的一道斜坡,在坡顶灯杆CD的顶端D处有一探射灯,射出的边缘光线DA和DB与水平路面AB所成的夹角∠DAN和∠DBN分别是37°和60°(图中的点A、B、C、D、M、N均在同一平面内,CM∥AN).
(1)求灯杆CD的高度;
(2)求AB的长度(结果精确到0.1米).(参考数据:
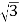 =1.73.sin37°≈060,cos37°≈0.80,tan37°≈0.75)
=1.73.sin37°≈060,cos37°≈0.80,tan37°≈0.75)
-
科目: 来源: 题型:
查看答案和解析>>【题目】重庆是一座美丽的山坡,某中学依山而建,校门A处,有一斜坡AB,长度为13米,在坡顶B处看教学楼CF的楼顶C的仰角∠CBF=53°,离B点4米远的E处有一花台,在E处仰望C的仰角∠CEF=63.4°,CF的延长线交校门处的水平面于D点,FD=5米.
(1)求斜坡AB的坡度i.
(2)求DC的长.
(参考数据:tan53°≈
 ,tan63.4°≈2)
,tan63.4°≈2)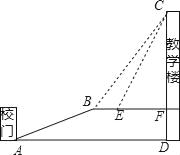
相关试题

