搜索
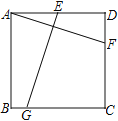
【题目】如图，在边长为6的正方形ABCD中，点F为CD上一点，E是AD的中点，且DF＝2．在BC上找点G，使EG＝AF，则BG的长是___________
参考答案：
【答案】1或5
【解析】
过E作EH⊥BC于H，取
，根据平行线分线段成比例定理得：BH=CH=3，证明Rt△ADF≌Rt△EHG，得GH=DF=2，可得BG的长，再运用等腰三角形的性质可得BG及
的长．
解：如图：过E作EH⊥BC于H，取 ,则AB∥EH∥CD，
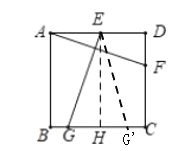
∵E是AD的中点，
∴BH=CH=3，
∵四边形ABCD是正方形，
∴AD=CD=EH，∠D=∠EHG=90°，
∵EG=AF，
∴Rt△ADF≌Rt△EHG(HL)，
∴GH=DF=2，
∴BG=BHGH=32=1；
∵
∴
∴
故答案为：1或5．
-
科目： 来源： 题型：
查看答案和解析>>【题目】如图，一次函数y＝kx+b（k≠0）的图象与反比例函数y＝
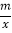（m≠0）的图象相交于C、D两点，和x轴交于A点，y轴交于B点．已知点C的坐标为（3，6），CD＝2BC．（1）求点D的坐标及一次函数的解析式；
（2）求△COD的面积．
-
科目： 来源： 题型：
查看答案和解析>>【题目】某地下车库出口处安装了“两段式栏杆”，如图1所示，点A是栏杆转动的支点，点E是栏杆两段的联结点．当车辆经过时，栏杆AEF最多只能升起到如图2所示的位置，其示意图如图3所示（栏杆宽度忽略不计），其中AB⊥BC，EF∥BC，∠AEF=143°，AB=AE=1.2米，那么适合该地下车库的车辆限高标志牌为（ ）（参考数据：sin37°≈0.60，cos37°≈0.80，tan37°≈0.75）
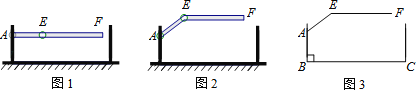
A．
B．
C．
D．
-
科目： 来源： 题型：
查看答案和解析>>【题目】某测量队在山脚A处测得山上树顶仰角为45°（如图），测量队在山坡上前进600米到D处，再测得树顶的仰角为60°，已知这段山坡的坡角为30°，如果树高为15米，则山高为（ ）（精确到1米，
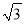=1.732）．
A. 585米 B. 1014米 C. 805米 D. 820米
-
科目： 来源： 题型：
查看答案和解析>>【题目】设θ为直角三角形的一个锐角，给出θ角三角函数的两条基本性质：①tanθ＝
；②cos2θ+sin2θ＝1，利用这些性质解答本题．已知cosθ+sinθ＝
，求值：(1)tanθ+
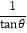； (2)|cosθ-sinθ|． -
科目： 来源： 题型：
查看答案和解析>>【题目】如图，在Rt△ABC中，∠C=90°，点D是BC边的中点，BD=2，tanB=
．（1）求AD和AB的长；
（2）求sin∠BAD的值．
-
科目： 来源： 题型：
查看答案和解析>>【题目】如图，BC是路边坡角为30°，长为10米的一道斜坡，在坡顶灯杆CD的顶端D处有一探射灯，射出的边缘光线DA和DB与水平路面AB所成的夹角∠DAN和∠DBN分别是37°和60°（图中的点A、B、C、D、M、N均在同一平面内，CM∥AN）．
（1）求灯杆CD的高度；
（2）求AB的长度（结果精确到0.1米）．（参考数据：
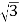=1.73．sin37°≈060，cos37°≈0.80，tan37°≈0.75）
相关试题
