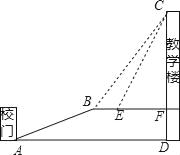
【题目】重庆是一座美丽的山坡,某中学依山而建,校门A处,有一斜坡AB,长度为13米,在坡顶B处看教学楼CF的楼顶C的仰角∠CBF=53°,离B点4米远的E处有一花台,在E处仰望C的仰角∠CEF=63.4°,CF的延长线交校门处的水平面于D点,FD=5米.
(1)求斜坡AB的坡度i.
(2)求DC的长.
(参考数据:tan53°≈![]() ,tan63.4°≈2)
,tan63.4°≈2)
参考答案:
【答案】(1)AB的坡度i=1:2.4;(2)DC=21米.
【解析】
过B作BG⊥AD于G,则四边形BGDF是矩形,求得BG=DF=5米,然后根据勾股定理求得AG,即可求得斜坡AB的坡度i.
在Rt△BCF中,BF=![]() ,在Rt△CEF中,EF=
,在Rt△CEF中,EF=![]() ,得到方程BF-EF=
,得到方程BF-EF=![]() -
-![]() =4,解得CF=16,即可求得求DC=21.
=4,解得CF=16,即可求得求DC=21.
知识点:
坡度:通常把坡面的垂直高度h和水平方向的距离l的比叫做坡度(或叫做坡比)用字母i表示。【即坡角的正切值(可写作:i=tan坡角=h:l)】
正切:把锐角A的对边与邻边的比叫做∠A的正切,记作tanA.
(1)过B作BG⊥AD于G,
则四边形BGDF是矩形,
∴BG=DF=5米,
∵AB=13米,
∴AG=![]() =12米,
=12米,
∴AB的坡度i=![]() =1:2.4;
=1:2.4;
(2)在Rt△BCF中,BF=![]() =
=![]() ,
,
在Rt△CEF中,EF=![]() =
=![]() ,
,
∵BE=4米,
∴BF﹣EF═![]() ﹣
﹣![]() =4,
=4,
解得:CF=16.
∴DC=CF+DF=16+5=21米.
-
科目: 来源: 题型:
查看答案和解析>>【题目】设θ为直角三角形的一个锐角,给出θ角三角函数的两条基本性质:①tanθ=
 ;②cos2θ+sin2θ=1,利用这些性质解答本题.已知cosθ+sinθ=
;②cos2θ+sin2θ=1,利用这些性质解答本题.已知cosθ+sinθ= ,求值:
,求值:(1)tanθ+
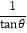 ; (2)|cosθ-sinθ|.
; (2)|cosθ-sinθ|. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在Rt△ABC中,∠C=90°,点D是BC边的中点,BD=2,tanB=
 .
.(1)求AD和AB的长;
(2)求sin∠BAD的值.

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,BC是路边坡角为30°,长为10米的一道斜坡,在坡顶灯杆CD的顶端D处有一探射灯,射出的边缘光线DA和DB与水平路面AB所成的夹角∠DAN和∠DBN分别是37°和60°(图中的点A、B、C、D、M、N均在同一平面内,CM∥AN).
(1)求灯杆CD的高度;
(2)求AB的长度(结果精确到0.1米).(参考数据:
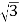 =1.73.sin37°≈060,cos37°≈0.80,tan37°≈0.75)
=1.73.sin37°≈060,cos37°≈0.80,tan37°≈0.75)
-
科目: 来源: 题型:
查看答案和解析>>【题目】观察与思考:阅读下列材料,并解决后面的问题
在锐角△ABC中,∠A、∠B、∠C的对边分别是a、b、c,过A作AD⊥BC于D(如图(1)),则sinB=
 ,sinC=
,sinC= ,即AD=csinB,AD=bsinC,于是csinB=bsinC,即
,即AD=csinB,AD=bsinC,于是csinB=bsinC,即 ,同理有:
,同理有: ,
, ,所以
,所以 .
.即:在一个三角形中,各边和它所对角的正弦的比相等在锐角三角形中,若已知三个元素(至少有一条边),运用上述结论和有关定理就可以求出其余三个未知元素.
根据上述材料,完成下列各题.

(1)如图(2),△ABC中,∠B=45°,∠C=75°,BC=60,则∠A= ;AC= ;
(2)自从去年日本政府自主自导“钓鱼岛国有化”闹剧以来,我国政府灵活应对,现如今已对钓鱼岛执行常态化巡逻.某次巡逻中,如图(3),我渔政204船在C处测得A在我渔政船的北偏西30°的方向上,随后以40海里/时的速度按北偏东30°的方向航行,半小时后到达B处,此时又测得钓鱼岛A在的北偏西75°的方向上,求此时渔政204船距钓鱼岛A的距离AB.(结果精确到0.01,
 ≈2.449)
≈2.449) -
科目: 来源: 题型:
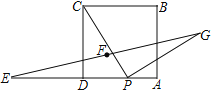
查看答案和解析>>【题目】如图,正方形ABCD的边长为4,点E为AD的延长线上一点,且DE=DC,点P为边AD上一动点,且PC⊥PG,PG=PC,点F为EG的中点.当点P从D点运动到A点时,则CF的最小值为___________
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在一条河的北岸有两个目标M、N,现在位于它的对岸设定两个观测点A、B.已知AB∥MN,在A点测得∠MAB=60°,在B点测得∠MBA=45°,AB=600米.
(1)求点M到AB的距离;(结果保留根号)
(2)在B点又测得∠NBA=53°,求MN的长.(结果精确到1米)
(参考数据:
 ≈1.732,sin53°≈0.8,cos53°≈0.6,tan53°≈1.33,cot53°≈0.75)
≈1.732,sin53°≈0.8,cos53°≈0.6,tan53°≈1.33,cot53°≈0.75)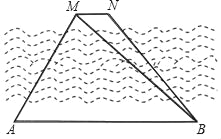
相关试题

