搜索
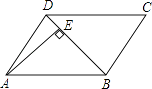
【题目】在Rt△ABC中，∠C=90°，c为斜边，a、b为直角边，则化简 
的结果为（ ）
A.3a+b﹣c
B.﹣a﹣3b+3c
C.a+3b﹣3c
D.2a
参考答案：
【答案】B
【解析】解：∵∠C=90°，c为斜边，a、b为直角边，
∴a+b＞c，a+c＞b，
∴原式=|a﹣b+c|﹣2|c﹣a﹣b|
=a﹣b+c+2（c﹣a﹣b）
=a﹣b+c+2c﹣2a﹣2b
=﹣a﹣3b+3c．
所以答案是：B．
【考点精析】本题主要考查了二次根式的性质与化简和三角形三边关系的相关知识点，需要掌握1、如果被开方数是分数（包括小数）或分式，先利用商的算数平方根的性质把它写成分式的形式，然后利用分母有理化进行化简．2、如果被开方数是整数或整式，先将他们分解因数或因式，然后把能开得尽方的因数或因式开出来；三角形两边之和大于第三边；三角形两边之差小于第三边；不符合定理的三条线段，不能组成三角形的三边才能正确解答此题．
-
科目： 来源： 题型：
查看答案和解析>>【题目】Rt△ABC中，∠C=90°，点D、E分别是△ABC边AC、BC上的点，点P是一动点．令∠PDA=∠1，∠PEB=∠2，∠DPE=∠α．
（1）若点P在线段AB上，如图（1）所示，且∠α=50°，则∠1+∠2= °；
（2）若点P在边AB上运动，如图（2）所示，则∠α、∠1、∠2之间有何关系？说明理由．
（3）若点P在Rt△ABC斜边BA的延长线上运动（CE＜CD），则∠α、∠1、∠2之间有何关系？猜想并说明理由．
-
科目： 来源： 题型：
查看答案和解析>>【题目】如图，平行四边形ABCD中，DB=DC，∠C=70°，AE⊥BD于E，则∠DAE等于（ ）
A.20°
B.25°
C.30°
D.35° -
科目： 来源： 题型：
查看答案和解析>>【题目】为了推动“龙江经济带”建设，我省某蔬菜企业决定通过加大种植面积、增加种植种类，促进经济发展，2017年春，预计种植西红柿、马铃薯、青椒共100公顷(三种蔬菜的种植面积均为整数)，青椒的种植面积是西红柿种植面积的2倍，经预算，种植西红柿的利润可达1万元/公顷，青椒1.5万元/公顷，马铃薯2万元/公顷，设种植西红柿x公顷，总利润为y万元．
(1)求总利润y(万元)与种植西红柿的面积x(公顷)之间的关系式．
(2)若预计总利润不低于180万元，西红柿的种植面积不低于8公顷，有多少种种植方案？
(3)在(2)的前提下，该企业决定投资不超过获得最大利润的
在冬季同时建造A、B两种类型的温室大棚，开辟新的经济增长点，经测算，投资A种类型的大棚5万元/个，B种类型的大棚8万元/个，请直接写出有哪几种建造方案？ -
科目： 来源： 题型：
查看答案和解析>>【题目】二次函数y=ax2+bx+c（a，b，c为常数，且a≠0）中的x与y的部分对应值如下表：
X
﹣1
0
1
3
y
﹣1
3
5
3
下列结论：
①ac＜0；
②当x＞1时，y的值随x值的增大而减小．
③3是方程ax2+（b﹣1）x+c=0的一个根；
④当﹣1＜x＜3时，ax2+（b﹣1）x+c＞0．
其中正确的个数为（ ）
A.4个
B.3个
C.2个
D.1个 -
科目： 来源： 题型：
查看答案和解析>>【题目】对于有理数a、b，定义运算：“★”，当a≥b时，a★b=2a-3b，当a＜b时，a★b=
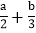．（1）计算：（x+2）★（x+1）的值；
（2）若（x+1）★（2x-1）=-1，求x的值．
-
科目： 来源： 题型：
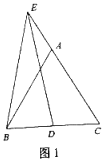
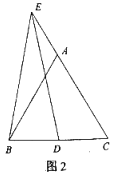
查看答案和解析>>【题目】如图1，△ABC是等边三角形，点D是BC上一点，点E在CA的延长线上，连结EB、ED，且EB=ED.
(1)求证:∠DEC=∠ABE；
(2)点D关于直线EC的对称点为M,连接EM、BM：
①依题意将图2补全；
②求证:EB=BM.
相关试题
