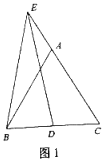
【题目】如图1,△ABC是等边三角形,点D是BC上一点,点E在CA的延长线上,连结EB、ED,且EB=ED.
(1)求证:∠DEC=∠ABE;
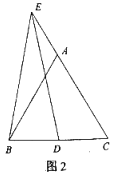
(2)点D关于直线EC的对称点为M,连接EM、BM:
①依题意将图2补全;
②求证:EB=BM.
参考答案:
【答案】(1)证明见解析;(2)①作图见解析;②证明见解析.
【解析】
(1)根据等边三角形的性质得到∠ABC=∠ACB=∠BAC=60°,再根据等边对等角以及三角形外角的性质即可得出结论;
(2)①根据题意作出图形即可;
②由轴对称的性质得到:DE=EM,DG=GM,再根据等腰三角形三线合一的性质得到∠2=∠1.由(1)的结论即可得到∠1=∠3.再证明△BEM是等边三角形即可得出结论.
(1)∵△ABC是等边三角形,∴∠ABC=∠ACB=∠BAC=60°.
∵BE=DE,∴∠EBD=∠EDB,∴∠EBA+∠ABC=∠CED+∠C,∴∠EBA =∠CED,即∠DEC=∠ABE;
(2)①作图如下:
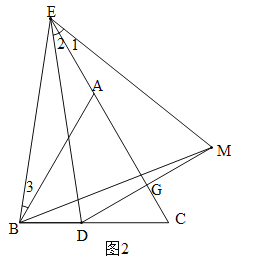
②∵D、M关于直线AC对称,∴DE=EM,DG=GM,∴∠2=∠1.由(1)得:∠2=∠3,∴∠1=∠3.
∵BE=DE,∴BE=ME.
∵∠3+∠BEA=∠BAC=60°,∴∠1+∠BEA=60°,∴∠BEM=60°.
∵BE=ME,∴△BEM是等边三角形,∴EB=BM.
-
科目: 来源: 题型:
查看答案和解析>>【题目】在Rt△ABC中,∠C=90°,c为斜边,a、b为直角边,则化简
 的结果为( )
的结果为( )
A.3a+b﹣c
B.﹣a﹣3b+3c
C.a+3b﹣3c
D.2a -
科目: 来源: 题型:
查看答案和解析>>【题目】二次函数y=ax2+bx+c(a,b,c为常数,且a≠0)中的x与y的部分对应值如下表:
X
﹣1
0
1
3
y
﹣1
3
5
3
下列结论:
①ac<0;
②当x>1时,y的值随x值的增大而减小.
③3是方程ax2+(b﹣1)x+c=0的一个根;
④当﹣1<x<3时,ax2+(b﹣1)x+c>0.
其中正确的个数为( )
A.4个
B.3个
C.2个
D.1个 -
科目: 来源: 题型:
查看答案和解析>>【题目】对于有理数a、b,定义运算:“★”,当a≥b时,a★b=2a-3b,当a<b时,a★b=
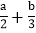 .
.(1)计算:(x+2)★(x+1)的值;
(2)若(x+1)★(2x-1)=-1,求x的值.
-
科目: 来源: 题型:
查看答案和解析>>【题目】为进一步加强和改进学校体育工作,切实提高学生体质健康水平,决定推进“一校一球队、一级一专项、一人一技能”活动计划,某校决定对学生感兴趣的球类项目(A:足球,B:篮球,C:排球,D:羽毛球,E:乒乓球)进行问卷调查,学生可根据自己的喜好选修一门,李老师对某班全班同学的选课情况进行统计后,制成了两幅不完整的统计图(如图)
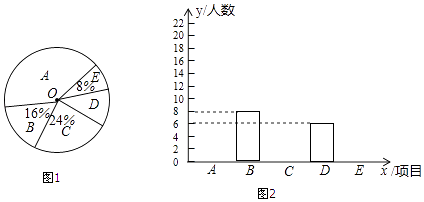
(1)将统计图补充完整
(2)求出该班学生人数
(3)若该校共用学生3500名,请估计有多少人选修足球?
(4)该班班委5人中,1人选修篮球,3人选修足球,1人选修排球,李老师要从这5人中任选2人了解他们对体育选修课的看法,请你用列表或画树状图的方法,求选出的2人恰好1人选修篮球,1人选修足球的概率 -
科目: 来源: 题型:
查看答案和解析>>【题目】胜利中学在一次健康知识竞赛活动中,抽取了一部分学生的测试成绩(成绩均为整数),整理后绘制成如图所示的频数直方图,根据图示信息,下列描述不正确的是( )
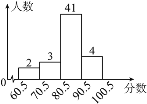
A. 抽查了50名学生
B. 成绩在60.5~70.5分范围的频数为2
C. 成绩在70.5~80.5分范围的频数比成绩在60.5~70.5分范围的频数多1
D. 成绩在70.5~80.5分范围的频率为0.8
-
科目: 来源: 题型:
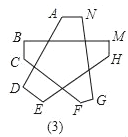
查看答案和解析>>【题目】“转化”是数学中的一种重要思想,即把陌生的问题转化成熟悉的问题,把复杂的问题转化成简单的问题,把抽象的问题转化为具体的问题.
(1)请你根据已经学过的知识求出下面星形图(1)中∠A+∠B+∠C+∠D+∠E的度数;
(2)若对图(1)中星形截去一个角,如图(2),请你求出∠A+∠B+∠C+∠D+∠E+∠F的度数;
(3)若再对图(2)中的角进一步截去,你能由题(2)中所得的方法或规律,猜想图3中的∠A+∠B+∠C+∠D+∠E+∠F+∠G+∠H+∠M+∠N的度数吗?只要写出结论,不需要写出解题过程)
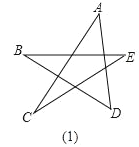
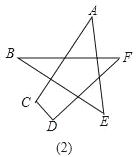
相关试题

