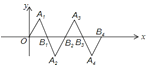
【题目】在如图所示的平面直角坐标系中,△OA1B1是边长为2的等边三角形,作△B2A2B1与△OA1B1关于点B1成中心对称,再作△B2A3B3与△B2A2B1关于点B2成中心对称,如此作下去,则△B2nA2n+1B2n+1(n是正整数)的顶点A2n+1的坐标是 。
参考答案:
【答案】(4n+1,![]() )
)
【解析】
试题分析:∵△OA1B1是边长为2的等边三角形,
∴A1的坐标为(1,![]() ),B1的坐标为(2,0),
),B1的坐标为(2,0),
∵△B2A2B1与△OA1B1关于点B1成中心对称,
∴点A2与点A1关于点B1成中心对称,
∵2×2﹣1=3,2×0﹣![]() =﹣
=﹣![]() ,
,
∴点A2的坐标是(3,﹣![]() ),
),
∵△B2A3B3与△B2A2B1关于点B2成中心对称,
∴点A3与点A2关于点B2成中心对称,
∵2×4﹣3=5,2×0﹣(﹣![]() )=
)=![]() ,
,
∴点A3的坐标是(5,![]() ),
),
∵△B3A4B4与△B3A3B2关于点B3成中心对称,
∴点A4与点A3关于点B3成中心对称,
∵2×6﹣5=7,2×0﹣![]() =﹣
=﹣![]() ,
,
∴点A4的坐标是(7,﹣![]() ),
),
…,
∵1=2×1﹣1,3=2×2﹣1,5=2×3﹣1,7=2×3﹣1,…,
∴An的横坐标是2n﹣1,A2n+1的横坐标是2(2n+1)﹣1=4n+1,
∵当n为奇数时,An的纵坐标是![]() ,当n为偶数时,An的纵坐标是﹣
,当n为偶数时,An的纵坐标是﹣![]() ,
,
∴顶点A2n+1的纵坐标是![]() ,
,
∴△B2nA2n+1B2n+1(n是正整数)的顶点A2n+1的坐标是(4n+1,![]() ).
).
-
科目: 来源: 题型:
查看答案和解析>>【题目】在△ABC中,AB=15,BC=14,AC=13,求△ABC的面积.
某学习小组经过合作交流,给出了下面的解题思路,请你按照他们的解题思路完成解答过程.
思路:(1) 作AD⊥BC于D,设BD = x,用含x的代数式表示CD;(2)根据勾股定理,利用AD作为“桥梁”,建立方程模型,求出x;(3)利用勾股定理求出AD的长,再计算三角形面积.

-
科目: 来源: 题型:
查看答案和解析>>【题目】某种出租车的收费标准是:起步价7元(即行驶距离不超过3km都需付7元车费);超过3km以后,每增加1km,加收2.4元(不足1km按1km计),某人乘出租车从甲地到乙地共支付车费19元,则此人从甲地到乙地经过的路程( ).
A. 正好8km B. 最多8km
C. 至少8km D. 正好7km
-
科目: 来源: 题型:
查看答案和解析>>【题目】若2x+5与9﹣3x互为相反数,则x﹣2的值为_____.
-
科目: 来源: 题型:
查看答案和解析>>【题目】用科学记数法表示927 000正确的是( )
A.9.27×106B.9.27×105C.9.27×104D.927×103
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,将
 ABCD的边AB延长到点E,使BE=AB,连接DE,交边BC于点F.
ABCD的边AB延长到点E,使BE=AB,连接DE,交边BC于点F.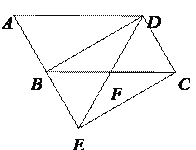
(1)求证:△BEF≌△CDF.
(2)连接BD,CE,若∠BFD=2∠A,求证四边形BECD是矩形.
-
科目: 来源: 题型:
查看答案和解析>>【题目】下列计算正确的是( )
A.5ab﹣3b=2aB.2a2b÷b=2a2(b≠0)
C.(a﹣1)2=a2﹣1D.(﹣3a2b)2=6a4b2
相关试题

