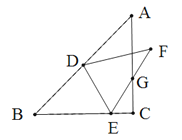
【题目】如图,△ABC中,∠ACB=90°,AB=2,BC=AC,D为AB的中点,E为BC上一点,将△BDE沿DE翻折,得到△FDE,EF交AC于点G,则△ECG的周长是___________.
参考答案:
【答案】![]()
【解析】
连接CE.根据“直角三角形斜边上的中线等于斜边的一半”、等腰三角形的性质以及折叠的性质推知EG+CG=EG+GF=EF=BE,
解:(1)如图,连接CD、CF.
∵Rt△ABC中,∠ACB=90°,AC=BC,D为AB边的中点,
∴BD=CD=1.BC=![]() ,
,
∵由翻折可知BD=DF,
∴CD=BD=DF=1,∠DFE=∠B=∠DCA=45°,
∴∠DCF=∠DFC,
∴∠DCF-∠DCA=∠DFC-∠DFE,即∠GCF=∠GFC,
∴GC=GF,
∴EG+CG=EG+GF=EF=BE,
∴△ECG的周长=EG+GC+CE=BE+EC=BC=![]() ,
,
故答案为:![]() .
.
-
科目: 来源: 题型:
查看答案和解析>>【题目】二次函数图象的顶点在原点O,经过点A(1,
 );点F(0,1)在y轴上.直线y=﹣1与y轴交于点H.
);点F(0,1)在y轴上.直线y=﹣1与y轴交于点H.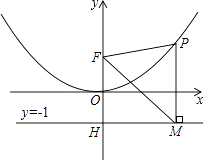
(1)求二次函数的解析式;
(2)点P是(1)中图象上的点,过点P作x轴的垂线与直线y=﹣1交于点M,求证:FM平分∠OFP;
(3)当△FPM是等边三角形时,求P点的坐标. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,等腰三角形ABC的底边BC长为4,面积是16,腰AC的垂直平分线EF分别交AC,AB边于E,F点
 若点D为BC边的中点,点M为线段EF上一动点,则
若点D为BC边的中点,点M为线段EF上一动点,则 周长的最小值为
周长的最小值为


A. 6 B. 8 C. 10 D. 12
-
科目: 来源: 题型:
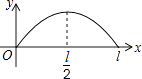
查看答案和解析>>【题目】点P从点O出发,按逆时针方向沿周长为l的图形运动一周,O,P两点间的距离y与点P走过的路程x的函数关系如图,那么点P所走的图形是( )

A.
B.
C.
D.
-
科目: 来源: 题型:
查看答案和解析>>【题目】点P从点O出发,按逆时针方向沿周长为l的图形运动一周,O,P两点间的距离y与点P走过的路程x的函数关系如图,那么点P所走的图形是( )
A.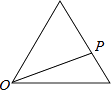
B.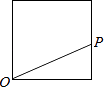
C.
D.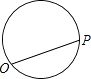
-
科目: 来源: 题型:
查看答案和解析>>【题目】(1)计算:∣1-
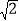 ∣+
∣+ 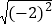 -(π-3.14)0
-(π-3.14)0(2)已知 (x-1)2 =16,求x的值
(3)已知8(x-1)3 -27=0,求x的值
-
科目: 来源: 题型:
查看答案和解析>>【题目】在ABCD中,SABCD=24,AE平分∠BAC,交BC于E,沿AE将△ABE折叠,点B的对应点为F,连接EF并延长交AD于G,EG将ABCD分为面积相等的两部分.则S△ABE= .
相关试题

