【题目】如图,△ABC中,AD⊥BC于点D,BE平分∠ABC,若∠ABC=64°,∠AEB=70°.
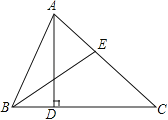
(1)求∠CAD的度数;
(2)若点F为线段BC上的任意一点,当△EFC为直角三角形时,求∠BEF的度数.
参考答案:
【答案】(1)52°;(2)58°或20°
【解析】
试题分析:(1)由角平分线得出∠EBC,得出∠BAD=26°,再求出∠C,即可得出∠CAD=52°;
(2)分两种情况:①当∠EFC=90°时;②当∠FEC=90°时;由角的互余关系和三角形的外角性质即可求出∠BEF的度数.
(1)证明:∵BE平分∠ABC,
∴∠ABC=2∠EBC=64°,
∴∠EBC=32°,
∵AD⊥BC,
∴∠ADB=∠ADC=90°,
∴∠BAD=90°﹣64°=26°,
∵∠C=∠AEB﹣∠EBC=70°﹣32°=38°,
∴∠CAD=90°﹣38°=52°;
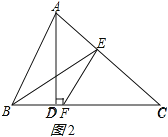
(2)解:分两种情况:
①当∠EFC=90°时,如图1所示:
则∠BFE=90°,
∴∠BEF=90°﹣∠EBC=90°﹣32°=58°;
②当∠FEC=90°时,如图2所示:
则∠EFC=90°﹣38°=52°,
∴∠BEF=∠EFC﹣∠EBC=52°﹣32°=20°;
综上所述:∠BEF的度数为58°或20°.

-
科目: 来源: 题型:
查看答案和解析>>【题目】某天,一蔬菜经营户用60元钱从蔬菜批发市场批了西红柿和豆角共40㎏到菜市场去卖,西红柿和豆角这天的批发价与零售价如下表所示:问:他当天卖完这些西红柿和豆角能赚多少钱?
品名
西红柿
豆角
批发价(单位:元/kg)
1.2
1.6
零售价(单位:元/kg)
1.8
2.5
-
科目: 来源: 题型:
查看答案和解析>>【题目】在下列语句中:
①由∠A:∠B:∠C=4:3:2可确定△ABC是锐角三角形;
②若三角形的两边长是3和4,且周长是偶数,则这个三角形的第三边是3或5;
③一个图形和它经过平移所得的图形中,两组对应点的连线互相平行;
④若一个多边形的外角和是内角和的
 ,则这个多边形是十二边形.
,则这个多边形是十二边形.其中正确的是_________(只要写序号).
-
科目: 来源: 题型:
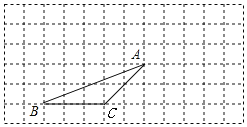
查看答案和解析>>【题目】如图,△ABC的顶点都在方格纸的格点上,将△ABC向右平移4格,再向上平移2格,其中每个格子的边长为1个单位长度.
(1)在图中画出平移后的△A′B′C′;
(2)若连接AA′、CC′,则这两条线段的关系是________;
(3)利用格点作直线MN,将△ABC分成面积相等的三角形.
-
科目: 来源: 题型:
查看答案和解析>>【题目】在宿州十一中校园文化艺术节中,九年级十班有1名男生和2名女生获得美术奖,另有2名男生和2名女生获得音乐奖.
(1)从获得美术奖和音乐奖的7名学生中选取1名参加颁奖大会,求刚好是男生的概率;
(2)分别从获得美术奖、音乐奖的学生中各选取1名参加颁奖大会,用列表或树状图求刚好是一男生一女生的概率.
-
科目: 来源: 题型:
查看答案和解析>>【题目】在学习了全等三角形和等边三角形的知识后,张老师出了如下一道题:如图,点B是线段AC上任意一点,分别以AB、BC为边在AC同一侧作等边△ABD和等边△BCE,连接CD、AE分别与BE和DB交于点N、M,连接MN.求证:△ABE≌△DBC.
接着张老师又让学生分小组进行探究:你还能得出什么结论?
精英小组探究的结论是:AM=DN
奋斗小组探究的结论是:△EMB≌△CNB.
创新小组探究的结论是:MN∥AC.
(1)你认为哪一小组探究的结论是正确的?
(2)选择其中你认为正确的一种情形加以证明.

-
科目: 来源: 题型:
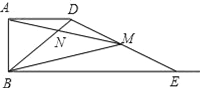
查看答案和解析>>【题目】如图,已知AB=2,AD=4,∠DAB=90°,AD∥BC.E是射线BC上的动点(点E与点B不重合),M是线段DE的中点,连结BD,交线段AM于点N,如果以A,N,D为顶点的三角形与△BME相似,则线段BE的长为___________.
相关试题

