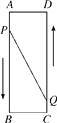
【题目】如图,已知A,B,C,D为矩形的四个顶点,AB=16 cm,AD=6 cm,动点P,Q分别从点A,C同时出发,点P以3 cm/s的速度向点B移动,一直到点B为止,点Q以2 cm/s的速度向点D移动,当点P停止运动时,点Q也停止运动.问:
(1)P,Q两点从开始出发多长时间时,四边形PBCQ的面积是33 cm2?
(2)P,Q两点从开始出发多长时间时,点P与点Q之间的距离是10 cm?
参考答案:
【答案】(1) P,Q两点从开始出发5s时,四边形PBCQ的面积是33cm2;(2) P,Q两点从开始出发1.6s或4.8s时,点P与点Q之间的距离是10cm.
【解析】试题分析:(1)、首先设xs时面积为33,然后根据梯形的面积计算法则列出方程,从而求出答案;(2)、过点Q作QH⊥AB于H,然后求出PH的长度,最后根据Rt△PHQ的勾股定理求出未知数的值得出答案.
试题解析:解:(1)设P,Q两点从开始出发xs时,四边形PBCQ的面积是33cm2.
则由题意得![]() ×(16-3x+2x)×6=33,
×(16-3x+2x)×6=33,
解得x=5.(3分)∵16÷3=![]() >5,
>5,
∴x=5符合题意.
故P,Q两点从开始出发5s时,四边形PBCQ的面积是33cm2;
(2)设P,Q两点从开始出发ys时,点P与Q之间的距离是10cm,
过点Q作QH⊥AB于H,

∴∠QHA=90°.∵四边形ABCD是矩形,∴∠A=∠D=90°,
∴四边形ADQH是矩形,∴AH=DQ=(16-2y)cm,QH=AD=6cm,
∴当P点在H点上方时,PH=AH-AP=16-2y-3y=(16-5y)(cm);当P点在H点下方时,PH=AP-AH=3y-(16-2y)=(5y-16)(cm), ∴PH=|16-5y|cm.
在Rt△PQH中,根据勾股定理得PH2+QH2=PQ2,
即(16-5y)2+62=102,解得y1=1.6,y2=4.8. ∵16÷3=![]() ,
,
∴y1=1.6和y2=4.8均符合题意.
故P,Q两点从开始出发1.6s或4.8s时,点P与点Q之间的距离是10cm.
-
科目: 来源: 题型:
查看答案和解析>>【题目】(1)观察下列各式:


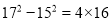 ……
……你发现了什么规律?试用你发现的规律填空:
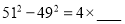 ;
;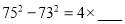
(2)请你用含一个字母的等式将上面各式呈现的规律表示出来,并用所学数学知识说明你所写式子的正确性.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知:两个等腰直角三角形(
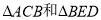 )边长分别为a和b(
)边长分别为a和b( )如图放置在一起,连接AD,
)如图放置在一起,连接AD,
(1)求阴影部分(
 )的面积
)的面积 (2)如果有一个
 点正好位于线段
点正好位于线段 的中点,连接
的中点,连接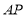 .
. 得到
得到 ,求
,求 的面积
的面积(3)(2)中的三角形
 比(1)中的
比(1)中的 面积大还是小,大(小)多少?
面积大还是小,大(小)多少? -
科目: 来源: 题型:
查看答案和解析>>【题目】从谢家集到田家庵有3路,121路,26路三条不同的公交线路.为了解早高峰期间这三条线路上的公交车从谢家集到田家庵的用时时间,在每条线路上随机选取了450个班次的公交车,收集了这些班次的公交车用时(单位:分钟)的数据,统计如下:
用时的频数 用时
线路



合计
3路
260
167
23
450
121路
160
166
124
450
26路
50
122
278
450
早高峰期间,乘坐__________(“3路”,“121路”或“26路”)线路上的公交车,从谢家集到田家庵“用时不超过50分钟”的可能性最大.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知关于x的一元二次方程x2+(m+3)x+m+1=0.
(1)求证:无论m取何值,原方程总有两个不相等的实数根:
(2)若x1,x2是原方程的两根,且|x1﹣x2|=2
 ,求m的值,并求出此时方程的两根.
,求m的值,并求出此时方程的两根. -
科目: 来源: 题型:
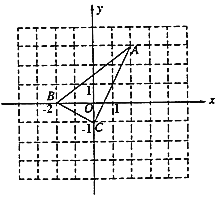
查看答案和解析>>【题目】如图,直角坐标系中的网格由单位正方形构成,
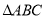 中,
中,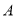 点坐标为
点坐标为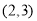 ,
,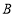 点坐标为
点坐标为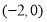 ,
,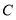 点坐标为
点坐标为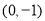 .
.
(1)
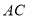 的长为_______;
的长为_______; (2)求证:
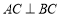 ;
; (3)若以
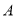 、
、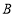 、
、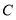 及点
及点 为顶点的四边形为平行四边形,写出
为顶点的四边形为平行四边形,写出 点在第一象限时的坐标______.
点在第一象限时的坐标______. -
科目: 来源: 题型:
查看答案和解析>>【题目】为了解社区居民最喜欢的支付方式,某兴趣小组对龙湖社区内20~60岁年龄段的部分居民展开了随机问卷调查(每人只能选择其中一项),并将调查数据整理后绘成如下两幅不完整的统计图.请根据图中信息解答下列问题:

(1)求参与问卷调查的总人数.
(2)补全条形统计图.
(3)该社区中20~60岁的居民约4000人,估算这些人中最喜欢微信支付方式的人数.
相关试题

