搜索
【题目】一个多边形的每一个外角为30°，那么这个多边形的边数为_____．
参考答案：
【答案】12
【解析】
一个正多边形的每个内角都相等，根据内角与外角互为邻补角，因而就可以求出外角的度数．根据任何多边形的外角和都是360°，利用360°除以外角的度数就可以求出外角和中外角的个数，即多边形的边数．
多边形的边数：360°÷30°＝12，
则这个多边形的边数为12．
故答案为：12．
-
科目： 来源： 题型：
查看答案和解析>>【题目】先化简，再求值：（﹣2x2+6+3x）+（6x﹣3+3x2），其中x＝﹣2．
-
科目： 来源： 题型：
查看答案和解析>>【题目】点M（2，﹣3）到x轴的距离是（ ）
A.2
B.﹣3
C.3
D.以上都不对 -
科目： 来源： 题型：
查看答案和解析>>【题目】如图，已知∠AOB是直角，OE平分∠AOC，OF平分∠BOC．
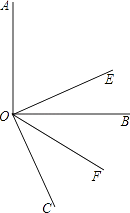
（1）若∠BOC=60°，求∠EOF的度数；
（2）若∠AOC=x°（x＞90），此时能否求出∠EOF的大小，若能请求出它的数值；若不能，请用含x的代数式来表示． -
科目： 来源： 题型：
查看答案和解析>>【题目】已知线段AB=30cm．
（1）如图1，点P沿线段AB自点A向点B以2cm/s的速度运动，同时点Q沿线段BA自点B向点A以3cm/s的速度运动，几秒钟后，P，Q两点相遇？
（2）几秒后，点P、Q两点相距10cm？
（3）如图2，AO=PO=4cm，∠POB=60°，现点P绕着点O以30°/秒的速度逆时针旋转一周停止，同时点Q沿直线B自B点向A点运动，假若点P，Q两点能相遇，求点Q的运动速度．
-
科目： 来源： 题型：
查看答案和解析>>【题目】计算下列各题：
（1）（﹣3）×（﹣
）÷（﹣1 
）
（2）48×（
）﹣（﹣48）÷（﹣8）
（3）（﹣1）2013﹣22﹣|﹣ |×（﹣10）2﹣19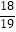 
×19 （用简便方法计算） -
科目： 来源： 题型：
查看答案和解析>>【题目】下列运算正确的是（ ）
A.a4+a2＝a6B.（m﹣n）2＝m2﹣n2C.（x2y）3＝x6y3D.b6÷b2＝b3
相关试题
