搜索
【题目】函数y=
(k＞0)的图象上两点A(x1, y1)和B(x2, y2),且x1＞x2＞0，分别过A、B向x轴作AA1⊥x轴于A1，BB1⊥x轴于B1，则
_________
(填“＞”“=”或“＜”)，若
=2，则函数解析式为_________.
参考答案：
【答案】 ＝ y=
【解析】解：两点A（x1，y1）和B（x2，y2），在函数
（k＞0）的图象上，因而代入得到：k=x1y1=x2y2，则
=
x1y1， 
=
x2y2，则
=
；
设A点的坐标是（m，n），则S△AA1O=
mn=2，则mn=4，设函数的解析式是
，A点的坐标是（m，n）一定满足函数解析式，得到p=mn=4，则函数解析式为
．
则
=
（填“＞”“=”或“＜”），若
=2，则函数解析式为
．
故答案为：=； 
．
-
科目： 来源： 题型：
查看答案和解析>>【题目】如图，以AB为直径的⊙O经过点P，C是⊙O上一点，连接PC交AB于点E，且∠ACP=60°，PA=PD．
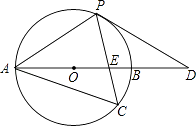
（1）试判断PD与⊙O的位置关系，并说明理由；
（2）若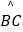
： 
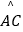=1：2，求AE：EB：BD的值（请你直接写出结果）；
（3）若点C是弧AB的中点，已知AB=4，求CECP的值． -
科目： 来源： 题型：
查看答案和解析>>【题目】4月的某天小欣在“A超市”买了“雀巢巧克力”和“趣多多小饼干”共10包，已知“雀巢巧克力”每包22元，“趣多多小饼干”每包2元，总共花费了80元．
（1）请求出小欣在这次采购中，“雀巢巧克力”和“趣多多小饼干”各买了多少包？
（2）“五一”期间，小欣发现，A、B两超市以同样的价格出售同样的商品，并且又各自推出不同的优惠方案：在A超市累计购物超过50元后，超过50元的部分打九折；在B超市累计购物超过100元后，超过100元的部分打八折．
①请问“五一”期间，若小欣购物金额超过100元，去哪家超市购物更划算？
②“五一”期间，小欣又到“B超市”购买了一些“雀巢巧克力”，请问她至少购买多少包时，平均每包价格不超过20元？
-
科目： 来源： 题型：
查看答案和解析>>【题目】如图，在直角坐标平面中，O为原点，点A的坐标为（20，0），点B在第一象限内，BO=10，sin∠BOA=
． 
（1）在图中，求作△ABO的外接圆（尺规作图，不写作法但需保留作图痕迹）；
（2）求点B的坐标与cos∠BAO的值；
（3）若A，O位置不变，将点B沿x轴向右平移使得△ABO为等腰三角形，请求出平移后点B的坐标． -
科目： 来源： 题型：
查看答案和解析>>【题目】如图，在平面直角坐标系中，点A，B的坐标分别为A（0，a），B（b，a），且a、b满足（a﹣2）2+|b﹣4|=0，现同时将点A，B分别向下平移2个单位，再向左平移1个单位，分别得到点A，B的对应点C，D，连接AC，BD，AB．
（1）求点C，D的坐标及四边形ABDC的面积S四边形ABCD；
（2）在y轴上是否存在一点M，连接MC，MD，使S△MCD=
S四边形ABDC？若存在这样一点，求出点M的坐标，若不存在，试说明理由；（3）点P是直线BD上的一个动点，连接PA，PO，当点P在BD上移动时（不与B，D重合），直接写出∠BAP、∠DOP、∠APO之间满足的数量关系．
-
科目： 来源： 题型：
查看答案和解析>>【题目】如图，已知点A的坐标是（﹣1，0），点B的坐标是（9，0），以AB为直径作⊙O′，交y轴的负半轴于点C，连接AC、BC，过A、B、C三点作抛物线．
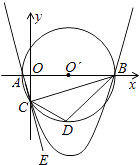
（1）求点C的坐标及抛物线的解析式；
（2）点E是AC延长线上一点，∠BCE的平分线CD交⊙O′于点D，求点D的坐标；并直接写出直线BC、直线BD的解析式；
（3）在（2）的条件下，抛物线上是否存在点P，使得∠PDB=∠CBD，若存在，请求出点P的坐标，若不存在，请说明理由． -
科目： 来源： 题型：
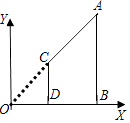
查看答案和解析>>【题目】如图，AB，CD都垂直于x轴，垂足分别为B，D，若A（6，3），C（2，1）， 则△OCD与四边形ABDC的面积比为（ ）
A.1：2
B.1：3
C.1：4
D.1：8
相关试题
