【题目】如图,以AB为直径的⊙O经过点P,C是⊙O上一点,连接PC交AB于点E,且∠ACP=60°,PA=PD. 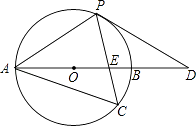
(1)试判断PD与⊙O的位置关系,并说明理由;
(2)若 ![]() :
: ![]() =1:2,求AE:EB:BD的值(请你直接写出结果);
=1:2,求AE:EB:BD的值(请你直接写出结果);
(3)若点C是弧AB的中点,已知AB=4,求CECP的值.
参考答案:
【答案】
(1)解:PD与⊙O相切.理由如下:
连接OP,
∵∠ACP=60°,
∴∠AOP=120°,
而OA=OP,
∴∠PAO=∠APO=30°,
∵PA=PD,
∴∠D=∠PAD=30°,
∴∠APD=180°﹣30°﹣30°=120°,
∴∠OPD=120°﹣30°=90°,
∵OP为半径,
∴PD是⊙O的切线
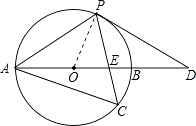
(2)解:连BC,
∵AB为直径,
∴∠ACB=90°,
∵ ![]() :
: ![]() =1:2,
=1:2,
∴∠ABC=2∠BAC,
∴∠BAC=30°,∠ABC=60°,
而∠PAE=30°,
∴∠APE=∠DPE=60°,
∴AE垂直平分PC,如图,
设BE=x,在Rt△BCE中,∠BCE=30°,则BC=2BE=2x,
在Rt△ABC中,∠CAB=30°,AB=2BC=4x,
∴AE=AB﹣BE=3x,
∵PA=PD,PE⊥AD,
∴AE=DE,
∴DB=3x﹣x=2x,
∴AE:EB:BD的值为3:1:2
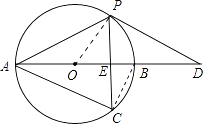
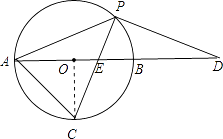
(3)解:如图,连接OC,
∵弧AC=弧BC,CO⊥AD,
∴∠CAB=∠APC,OC⊥AB,
而∠ACE=∠PCA,
∴△ACE∽△PCA,
∴ ![]() ,即AC2=PCCE,
,即AC2=PCCE,
∵A02+OC2=AC2=8,
∴PCCE=AC2=8.
【解析】(1)连OP,根据圆周角定理得到∠AOP=2∠ACP=120°,则∠PAO=∠APO=30°,利用PA=PD得到∠D=∠PAD=30°,则∠APD=180°﹣30°﹣30°=120°,于是得到∠OPD=120°﹣30°=90°,根据切线的判定定理即可得到PD是⊙O的切线;(2)连BC,由AB为直径,根据直径所对的圆周角为直角得到∠ACB=90°,利用 ![]() :
: ![]() =1:2,则∠ABC=2∠BAC,所以有∠BAC=30°,∠ABC=60°,而∠PAE=30°,得到AE垂直平分PC,设BE=x,然后利用含30°的直角三角形三边的关系可求出AE:EB:BD的值;(3)根据圆周角定理由弧AC=弧BC,得到∠CAB=∠APC,OC⊥AB,根据相似三角形的判定方法易得△ACE∽△PCA,则
=1:2,则∠ABC=2∠BAC,所以有∠BAC=30°,∠ABC=60°,而∠PAE=30°,得到AE垂直平分PC,设BE=x,然后利用含30°的直角三角形三边的关系可求出AE:EB:BD的值;(3)根据圆周角定理由弧AC=弧BC,得到∠CAB=∠APC,OC⊥AB,根据相似三角形的判定方法易得△ACE∽△PCA,则 ![]() ,即AC2=PCCE,利用勾股定理有A02+OC2=AC2=8,即可得到CECP的值.
,即AC2=PCCE,利用勾股定理有A02+OC2=AC2=8,即可得到CECP的值.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,水坝的横断面是梯形,背水坡AB的坡角∠BAD=60°,坡长AB=20
 m,为加强水坝强度,降坝底从A处后水平延伸到F处,使新的背水坡角∠F=45°,求AF的长度(结果精确到1米,参考数据:
m,为加强水坝强度,降坝底从A处后水平延伸到F处,使新的背水坡角∠F=45°,求AF的长度(结果精确到1米,参考数据:  1.414,
1.414,  ≈1.732).
≈1.732).
-
科目: 来源: 题型:
查看答案和解析>>【题目】某商场对一种新售的手机进行市场问卷调查,其中一个项目是让每个人按A(不喜欢)、B(一般)、C(不比较喜欢)、D(非常喜欢)四个等级对该手机进行评价,图①和图②是该商场采集数据后,绘制的两幅不完整的统计图,请你根据以上统计图提供的信息,回答下列问题:
(1)本次调查的人数为多少人?A等级的人数是多少?请在图中补全条形统计图.
(2)图①中,a等于多少?D等级所占的圆心角为多少度?

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,若把边长为1的正方形ABCD的四个角(阴影部分)剪掉,得一四边形A1B1C1D1 . 试问怎样剪,才能使剩下的图形仍为正方形,且剩下图形的面积为原来正方形面积的
 ,请说明理由.(写出证明及计算过程)
,请说明理由.(写出证明及计算过程) 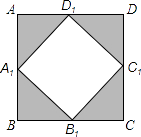
-
科目: 来源: 题型:
查看答案和解析>>【题目】4月的某天小欣在“A超市”买了“雀巢巧克力”和“趣多多小饼干”共10包,已知“雀巢巧克力”每包22元,“趣多多小饼干”每包2元,总共花费了80元.
(1)请求出小欣在这次采购中,“雀巢巧克力”和“趣多多小饼干”各买了多少包?
(2)“五一”期间,小欣发现,A、B两超市以同样的价格出售同样的商品,并且又各自推出不同的优惠方案:在A超市累计购物超过50元后,超过50元的部分打九折;在B超市累计购物超过100元后,超过100元的部分打八折.
①请问“五一”期间,若小欣购物金额超过100元,去哪家超市购物更划算?
②“五一”期间,小欣又到“B超市”购买了一些“雀巢巧克力”,请问她至少购买多少包时,平均每包价格不超过20元?
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在直角坐标平面中,O为原点,点A的坐标为(20,0),点B在第一象限内,BO=10,sin∠BOA=
 .
. 
(1)在图中,求作△ABO的外接圆(尺规作图,不写作法但需保留作图痕迹);
(2)求点B的坐标与cos∠BAO的值;
(3)若A,O位置不变,将点B沿x轴向右平移使得△ABO为等腰三角形,请求出平移后点B的坐标. -
科目: 来源: 题型:
查看答案和解析>>【题目】函数y=
 (k>0)的图象上两点A(x1, y1)和B(x2, y2),且x1>x2>0,分别过A、B向x轴作AA1⊥x轴于A1,BB1⊥x轴于B1,则
(k>0)的图象上两点A(x1, y1)和B(x2, y2),且x1>x2>0,分别过A、B向x轴作AA1⊥x轴于A1,BB1⊥x轴于B1,则 _________
_________ (填“>”“=”或“<”),若
(填“>”“=”或“<”),若 =2,则函数解析式为_________.
=2,则函数解析式为_________.
相关试题

