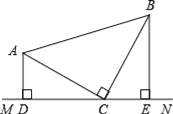
【题目】如图,在△ABC中∠ACB=90°,AC=BC,直线MN经过点C,且AD⊥MN于D,BE⊥MN于E.
(1)求证:△ADC≌△CEB;
(2)若AD=1,BE=2,求△ABC的面积.
参考答案:
【答案】见解析
【解析】
试题分析:
(1)如图,由已知易得在△ADC和△CEB中,AC=BC,∠ADC=∠CEB=90°,所有只需利用∠ACD+∠CAD=90°和∠ACD+∠BCE=90°,证得∠CAD=∠BCE就可以利用“角角边”证两三角形全等了;
(2)由(1)中结论:△ADC≌△CEB可得CE=AD=1,CD=BE=2,从而得到:DE=CD+CE=3,最后用梯形ABED的面积减去△ADC和△BCE的面积就可得到△ABC的面积.(学习“勾股定理”后也可利用“勾股定理”求得AC和BC的长直接计算△ABC的面积).
试题解析:
(1)证明:∵∠ACB=90°,∴∠ACD+∠BCE=90°,
又∵AD⊥MN,BE⊥MN,∴∠ADC=∠CEB=90°,
而∠ACD+∠DAC=90°,∴∠BCE=∠CAD.
在△ADC和△CEB中
∵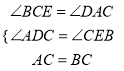 ,
,
∴△ADC≌△CEB(AAS).
(2)∵△ADC≌△CEB∴AD=CE,DC=EB.
又∵DE=DC+CE,∴DE=EB+AD=2+1=3.
∴△ABC的面积为: ![]() .
.
-
科目: 来源: 题型:
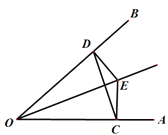
查看答案和解析>>【题目】如图,点E是∠AOB的平分线上一点,EC⊥OA,ED⊥OB,垂足分别为C、D,连接C、D.
(1)求证:OC=OD;
(2)请确定射线OE与线段CD 的位置关系,并说明理由.
-
科目: 来源: 题型:
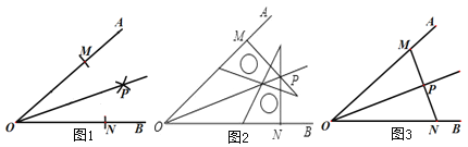
查看答案和解析>>【题目】(1)如图1,小明用尺规作图画∠AOB的角平分线OP,作图依据是__________(填写全等三角形的判定方法);
(2)如图2,小亮用直角三角尺按照下面的方法画∠AOB的角平分线:①在OA、OB上分别取点M、N,使OM=ON;②分别过点M、N画OA、OB的垂线,这两条垂线相交于点P;③画射线OP.则射线OP平分∠AOB.以上画角平分线,用到的三角形全等的判定方法是___________;
(3)如图3,小丽用刻度尺按照下面的方法画∠AOB的角平分线:①在OA、OB上分别取点M、N,使OM=ON;②连接M、N,取线段MN的中点P;③画射线OP.则射线OP平分∠AOB.请帮助小丽说明画图的正确性.
-
科目: 来源: 题型:
查看答案和解析>>【题目】把边长为3,5,7的两个全等三角形拼成四边形,一共能拼成____种不同的四边形,其中有____个平行四边形.
-
科目: 来源: 题型:
查看答案和解析>>【题目】在△ABC中,∠B,∠C的平分线交于点O,D是外角与内角平分线交点,E是外角平分线交点,若∠BOC=120°,则∠D=( )

A. 15° B. 20° C. 25° D. 30°
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在平面直角坐标系中,△AOB的顶点O为坐标原点,点A的坐标为(4,0),点B的坐标为(0,1),点C为边AB的中点,正方形OBDE的顶点E在x轴的正半轴上,连接CO,CD,CE.
(1)线段OC的长为 ;
(2)求证:△CBD≌△COE;
(3)将正方形OBDE沿x轴正方向平移得到正方形O1B1D1E1,其中点O,B,D,E的对应点分别为点O1,B1,D1,E1,连接CD,CE,设点E的坐标为(a,0),其中a≠2,△CD1E1的面积为S.
①当1<a<2时,请直接写出S与a之间的函数表达式;
②在平移过程中,当S=
 时,请直接写出a的值.
时,请直接写出a的值.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在不等边△ABC中,PM⊥AB于点M,PN⊥AC于点N,且PM=PN,Q在AC上,PQ=QA,MP=3,△AMP的面积是6,下列结论:①AM<PQ+QN,②QP∥AM,③△BMP≌△PQC,④∠QPC+∠MPB=90°,⑤△PQN的周长是7,其中正确的有( )个.
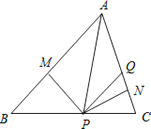
A. 1 B. 2 C. 3 D. 4
相关试题

