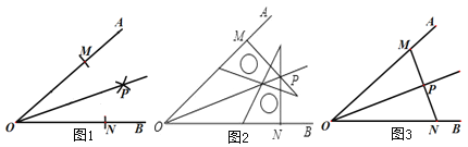
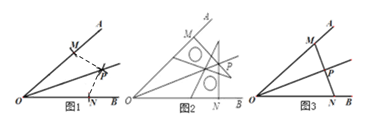
【题目】(1)如图1,小明用尺规作图画∠AOB的角平分线OP,作图依据是__________(填写全等三角形的判定方法);
(2)如图2,小亮用直角三角尺按照下面的方法画∠AOB的角平分线:①在OA、OB上分别取点M、N,使OM=ON;②分别过点M、N画OA、OB的垂线,这两条垂线相交于点P;③画射线OP.则射线OP平分∠AOB.以上画角平分线,用到的三角形全等的判定方法是___________;
(3)如图3,小丽用刻度尺按照下面的方法画∠AOB的角平分线:①在OA、OB上分别取点M、N,使OM=ON;②连接M、N,取线段MN的中点P;③画射线OP.则射线OP平分∠AOB.请帮助小丽说明画图的正确性.
参考答案:
【答案】 SSS HL
【解析】试题分析:(1)在图1中,连接MN和NP,由作图可知:OM=ON,MP=NP,又∵OP=OP,所以由“边边边”可证△OPM≌△OPN,从而得到∠AOP=∠BOP,∴作图依据是“SSS”;
(2)如图2,由已知条件和作图过程可知,OM=ON,∠OMP=∠ONP=90°,又∵OP=OP,∴由“HL”可证Rt△OPM≌Rt△OPN,从而得到∠AOP=∠BOP,∴用到的三角形全等判定方法是“HL”;
(3)如图3,由小丽的作法可知:OM=ON,PM=PN,又∵OP=OP,所以可由“SSS”证得△OPM≌△OPN,从而得到∠AOP=∠BOP,即OP平分∠AOB.
试题解析:
(1)如图1,连接MN和NP,由作图可知:OM=ON,MP=NP,又∵OP=OP,
∴ 在△OPM和△OPN中: 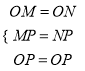 ,
,
∴ △OPM≌△OPN(SSS);
(2)如图2,由已知条件和作图过程可知,OM=ON,∠OMP=∠ONP=90°,
又∵OP=OP,
∴在Rt△OPM和Rt△OPN中: ![]() ,
,
∴Rt△OPM≌Rt△OPN(HL);
(3)∵点P是MN 的中点,∴PM=PN,
在△AOB和△DOC中: 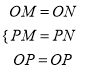 ,
,
∴△OPM≌△OPN(SSS)
∴∠POM=∠PON,即OP 是∠AOB的角平分线.
-
科目: 来源: 题型:
查看答案和解析>>【题目】从下列不等式中选一个与x+2≥1组成不等式组,若要使该不等式组的解集为x≥﹣1,则可以选择的不等式是( )
A. x>﹣2 B. x>0 C. x<0 D. x<﹣2
-
科目: 来源: 题型:
查看答案和解析>>【题目】将b3﹣4b分解因式,所得结果正确的是( )
A.b(b2﹣4)B.b(b﹣4)2
C.b(b﹣2)2D.b(b+2)(b﹣2)
-
科目: 来源: 题型:
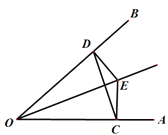
查看答案和解析>>【题目】如图,点E是∠AOB的平分线上一点,EC⊥OA,ED⊥OB,垂足分别为C、D,连接C、D.
(1)求证:OC=OD;
(2)请确定射线OE与线段CD 的位置关系,并说明理由.
-
科目: 来源: 题型:
查看答案和解析>>【题目】把边长为3,5,7的两个全等三角形拼成四边形,一共能拼成____种不同的四边形,其中有____个平行四边形.
-
科目: 来源: 题型:
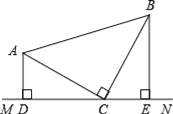
查看答案和解析>>【题目】如图,在△ABC中∠ACB=90°,AC=BC,直线MN经过点C,且AD⊥MN于D,BE⊥MN于E.
(1)求证:△ADC≌△CEB;
(2)若AD=1,BE=2,求△ABC的面积.
-
科目: 来源: 题型:
查看答案和解析>>【题目】在△ABC中,∠B,∠C的平分线交于点O,D是外角与内角平分线交点,E是外角平分线交点,若∠BOC=120°,则∠D=( )

A. 15° B. 20° C. 25° D. 30°
相关试题

