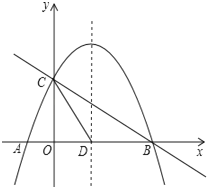
【题目】如图，抛物线与x轴交于A、B两点，与y轴交于点C，抛物线的对称轴交x轴于点D．

（1）求A、B、C、D的坐标；

（2）在抛物线的对称轴上是否存在点P，使△PCD是以CD为腰的等腰三角形？如果存在，直接写出P点的坐标；如果不存在，请说明理由；

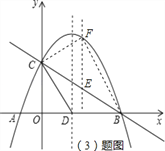
（3）点E（m，n）是线段BC上的一个动点，过点E作x轴的垂线与抛物线相交于点F，当点E运动到什么位置时，△CBF的面积最大？求出△CBF的最大面积及此时E点的坐标．

参考答案：

【答案】（1）A（﹣1，0），B（2，0），C（0，2），D（，0）；（2）存在，（ ，4）或（， ）或（，﹣）；（3）△CBF的面积最大为1，E（1，1）

【解析】试题分析：（1）令y=0，解关于x的一元二次方程即可得到点A、B的坐标，令x=0，求出y的值，即可得到点C的坐标，求出抛物线对称轴，然后写出点D的坐标；

（2）利用勾股定理求出CD，然后分①点C是顶角顶点时，利用等腰三角形三线合一的性质求解，②点D是顶角顶点时，分点P在点D的上方和下方两种情况写出点P的坐标；

（3）利用待定系数法求一次函数解析式求出直线BC的解析式，表示出EF，再根据S△CBF=S△CBE+S△BEF列式整理，然后根据二次函数的最值问题解答．

解：（1）令y=0，则-x2+x+2=0，

解得x1=-1，x2=2，

所以，A（-1，0），B（2，0），

令x=0，则y=2，

所以，点C（0，2），

对称轴为直线x= ，

所以，点D（，0）；

（2）由（1）可知，OC=2，OD=，

所以，CD=＝，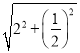

①点C是顶角顶点时，由等腰三角形三线合一的性质得，点P的纵坐标为点C的2倍，即2×2=4，

所以，点P的坐标为（，4），

②点D是顶角顶点时，若点P在点D的上方，则P（， ），

若点P在点D的下方，则P（， ），

综上所述，抛物线对称轴上存在点P（，4）或（， ）或（，﹣），使△PCD是以CD为腰的等腰三角形；

（3）可求直线BC的解析式为y=﹣x+2，

∵点E（m，n）是线段BC上的一个动点，过点E作x轴的垂线与抛物线相交于点F，

∴EF=﹣m2+m+2﹣（﹣m+2）=﹣m2+2m，

∴S△CBF=S△CEF+S△BEF= EF·OB =（﹣m2+2m）×2=﹣m2+2m=﹣（m﹣1）2+1，

∴当m=1时，△CBF的面积最大为1，此时，n=﹣1+2=1，所以，点E的坐标为（1，1）．

关闭