【题目】已知抛物线y=ax2+bx+c经过A(-1,0)、B(3,0)、C(0,3)三点,直线l是抛物线的对称轴.

(1)求抛物线的函数关系式;
(2)设点P是直线l上的一个动点,当△PAC的周长最小时,求点P的坐标;
参考答案:
【答案】(1)抛物线的解析式为:y=-x2+2x+3;(2) P点的坐标为(1,2).
【解析】试题分析:(1)根据函数图象经过的三点,用待定系数法确定二次函数的解析式即可;
(2)根据AC是定值,得到当PA+PC最小时,△PAC的周长最小,A点关于直线L的对称点为点B,连接BC交直线L与点P即可得.
试题解析:(1)将三点坐标分别代入解析式,解方程组得:a=-1 b=2 c=3,∴抛物线的解析式为:y=-x2+2x+3;
(2) ∵AC长为定值,∴当PA+PC值为最小时,△PAC的周长最小.
A点关于直线L的对称点为点B,连接BC交直线L与点P,P点的横坐标为1,
直线BC的解析式为:y=-x+3
∴当x=1时,y=2,∴P点的坐标为(1,2).
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,抛物线
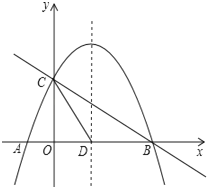
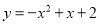 与x轴交于A、B两点,与y轴交于点C,抛物线的对称轴交x轴于点D.
与x轴交于A、B两点,与y轴交于点C,抛物线的对称轴交x轴于点D.(1)求A、B、C、D的坐标;
(2)在抛物线的对称轴上是否存在点P,使△PCD是以CD为腰的等腰三角形?如果存在,直接写出P点的坐标;如果不存在,请说明理由;
(3)点E(m,n)是线段BC上的一个动点,过点E作x轴的垂线与抛物线相交于点F,当点E运动到什么位置时,△CBF的面积最大?求出△CBF的最大面积及此时E点的坐标.
-
科目: 来源: 题型:
查看答案和解析>>【题目】点 M(-8,12)到 x 轴的距离是 ,到 y 轴的距离是 .
-
科目: 来源: 题型:
查看答案和解析>>【题目】为了了解学校开展“孝敬父母,从家务事做起”活动的实施情况,该校抽取八年级5名学生调查他们一周(按7天计算)做家务所用时间(单位:小时,调查结果保留一位小数),得到一组数据,并绘制成统计表,请根据表完成下列各题:
分组
划记
频数
频率
0.55~1.05
正正…
14
0.28
1.05~1.55
正正正
15
0.30
1.55~2.05
正…
7
2.05~2.55
…
4
0.08
2.55~3.05
…
5
0.10
3.05~3.55
…
3
3.55~4.05
T
0.04

(1)填写频率分布表中末完成的部分.
(2)由以上信息判断,每周做家务的时间不超过1.55h的学生所占的百分比是 .
(3)针对以上情况,写一个20字以内倡导“孝敬父母,热爱劳动”的句子. -
科目: 来源: 题型:
查看答案和解析>>【题目】某小区便民超市为了了解顾客的消费情况,在该小区居民中进行调查,询问每户人家每周到超市的次数,下图是根据调查结果绘制的,请问:

(1)这种统计图通常被称为什么统计图?
(2)此次调查共询问了多少户人家?
(3)超过半数的居民每周去多少次超市?
(4)请将这幅图改为扇形统计图. -
科目: 来源: 题型:
查看答案和解析>>【题目】某年级组织学生参加夏令营,分为甲、乙、丙三组进行活动.下面两幅统计图反映了学生报名参加夏令营的情况.请你根据图中的信息回答下列问题:


报名人数分布直方图 报名人数扇形统计图
(1)求该年级报名参加本次活动的总人数;
(2)求该年级报名参加乙组的人数,并补全频数分布直方图;
(3)根据实际情况,需从甲组抽调部分同学到丙组,使丙组人数是甲组人数的3倍,那么,应从甲组抽调多少名学生到丙组? -
科目: 来源: 题型:
查看答案和解析>>【题目】已知,∠1和∠2是一对内错角,且∠1=48°,那么∠2的度数是( )
A.48°
B.42°
C.132°
D.无法确定
相关试题

