Question

【题目】如图1，在平面直径坐标系中，抛物线y=ax2+bx﹣2与x轴交于点A（﹣3，0）．B（1，0），与y轴交于点C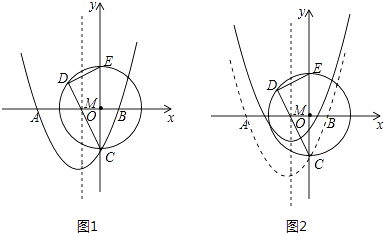

（1）直接写出抛物线的函数解析式；
（2）以OC为半径的⊙O与y轴的正半轴交于点E，若弦CD过AB的中点M，试求出DC的长；
（3）将抛物线向上平移 个单位长度（如图2）若动点P（x，y）在平移后的抛物线上，且点P在第三象限，请求出△PDE的面积关于x的函数关系式，并写出△PDE面积的最大值．

Answer 1

【答案】
（1）

解：将点A（﹣3，0）、B（1，0）代入y=ax2+bx﹣2中，

得： ，解得： ，

∴抛物线的函数解析式为y= x2+ x﹣2

（2）

解：令y= x2+ x﹣2中x=0，则y=﹣2，

∴C（0，﹣2），

∴OC=2，CE=4．

∵A（﹣3，0），B（1，0），点M为线段AB的中点，

∴M（﹣1，0），

∴CM= = ．

∵CE为⊙O的直径，

∴∠CDE=90°，

∴△COM∽△CDE，

∴ ，

∴DC= ．

（3）

解：将抛物线向上平移 个单位长度后的解析式为y= x2+ x﹣2+ = x2+ x﹣ ，

令y= x2+ x﹣ 中y=0，即 x2+ x﹣ =0，

解得：x1= ，x2= ．

∵点P在第三象限，

∴ ＜x＜0．

过点P作PP′⊥y轴于点P′，过点D作DD′⊥y轴于点D′，如图所示．

（方法一）：在Rt△CDE中，CD= ，CE=4，

∴DE= = ，sin∠DCE= = ，

在Rt△CDD′中，CD= ，∠CD′D=90°，

∴DD′=CDsin∠DCE= ，CD′= = ，

∴OD′=CD′﹣OC= ，

∴D（﹣ ， ），D′（0， ）．

∵P（x， x2+ x﹣ ），

∴P′（0， x2+ x﹣ ）．

∴S△PDE=S△DD′E+S梯形DD′P′P﹣S△EPP′= DD′ED′+ （DD′+PP′）D′P′﹣ PP′EP′=﹣ ﹣ x+2（ ＜x＜0），

∵S△PDE=﹣ ﹣ x+2=﹣ + ， ＜﹣ ＜0，

∴当x=﹣ 时，S△PDE取最大值，最大值为 ．

故：△PDE的面积关于x的函数关系式为S△PDE=﹣ ﹣ x+2（ ＜x＜0），且△PDE面积的最大值为 ．

（方法二）：在Rt△CDE中，CD= ，CE=4，

∴DE= = ，

∵∠CDE=∠CD′D=90°，∠DCE=∠D′CD，

∴△CDE∽△CD′D，

∴ = ，

∴DD′= ，CD′= ，

∴∴OD′=CD′﹣OC= ，

∴D（﹣ ， ），D′（0， ）．

∵P（x， x2+ x﹣ ），

∴P′（0， x2+ x﹣ ）．

∴S△PDE=S△DD′E+S梯形DD′P′P﹣S△EPP′= DD′ED′+ （DD′+PP′）D′P′﹣ PP′EP′=﹣ ﹣ x+2（ ＜x＜0），

∵S△PDE=﹣ ﹣ x+2=﹣ + ， ＜﹣ ＜0，

∴当x=﹣ 时，S△PDE取最大值，最大值为 ．

故：△PDE的面积关于x的函数关系式为S△PDE=﹣ ﹣ x+2（ ＜x＜0），且△PDE面积的最大值为 ．

【解析】（1）由点A、B的坐标利用待定系数法即可求出抛物线的解析式；（2）令抛物线解析式中x=0求出点C的坐标，根据点A、B的坐标即可求出其中点M的坐标，由此即可得出CM的长，根据圆中直径对的圆周角为90°即可得出△COM∽△CDE，根据相似三角形的性质即可得出 ，代入数据即求出DC的长度；（3）根据平移的性质求出平移后的抛物线的解析式，令其y=0，求出平移后的抛物线与x轴的交点坐标，由此即可得出点P横坐标的范围，再过点P作PP′⊥y轴于点P′，过点D作DD′⊥y轴于点D′，通过分割图形求面积法找出S△PDE关于x的函数关系式，利用配方结合而成函数的性质即可得出△PDE面积的最大值．
【考点精析】利用二次函数的性质对题目进行判断即可得到答案，需要熟知增减性：当a>0时，对称轴左边，y随x增大而减小；对称轴右边，y随x增大而增大；当a<0时，对称轴左边，y随x增大而增大；对称轴右边，y随x增大而减小．