【题目】将下列方格纸中的△ABC向右平移7格,再向下平移2格,得到△![]() .(1)画出平移后的三角形;
.(1)画出平移后的三角形;
(2)若AB=5,则![]() = .
= .
(3)连接AA1,BB1, 根据“图形平移”的性质,得:线段AA1与线段BB1的数量关系和位置关系是: .
(4)求图中∠![]() AC+∠
AC+∠![]() BC的度数.
BC的度数.

参考答案:
【答案】答案见解析
【解析】试题分析:(1)将A、B、C三点,分别向右平移7格,向下平移2格,然后顺次连接即可得到△![]() ;(2)根据平移的性质直接写出答案即可;(3)根据平移的性质直接写出答案即可;(4)利用SAS判定△ADA1≌BEB1,根据全等三角形的性质可得∠DAA1=∠EBB1,再由∠DAA1+∠CAA1=90°,即可得 ∠
;(2)根据平移的性质直接写出答案即可;(3)根据平移的性质直接写出答案即可;(4)利用SAS判定△ADA1≌BEB1,根据全等三角形的性质可得∠DAA1=∠EBB1,再由∠DAA1+∠CAA1=90°,即可得 ∠![]() AC+∠
AC+∠![]() BC=90°.
BC=90°.
试题解析:
(1)图形如下:
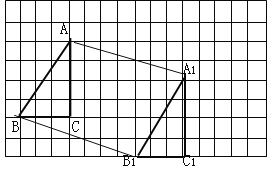
(2)![]() = 5 .
= 5 .
(3)AA1=BB1;AA1∥BB1;
(4)如图,利用SAS判定△ADA1≌BEB1,
∴∠DAA1=∠EBB1,∵∠DAA1+∠CAA1=90°,
∴∠![]() AC+∠
AC+∠![]() BC=90°.
BC=90°.
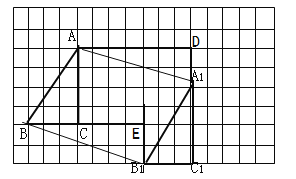
-
科目: 来源: 题型:
查看答案和解析>>【题目】某校七年级400名学生到郊外参加植树活动,已知用3辆小客车和1辆大客车每次可运送学生105人,用1辆小客车和2辆大客车每次可运送学生110人.
(1)每辆小客车和每辆大客车各能坐多少名学生?
(2)若计划租小客车m辆,大客车n辆,一次送完,且恰好每辆车都坐满:
①请你设计出所有的租车方案;
②若小客车每辆租金150元,大客车每辆租金250元,请选出最省线的租车方案,并求出最少租金.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在等边△ABC中,点E为边AB上任意一点,点D在边CB的延长线上,且ED=EC.

(1)当点E为AB的中点时(如图1),则有AE DB(填“>”“<”或“=”);
(2)猜想AE与DB的数量关系,并证明你的猜想.
-
科目: 来源: 题型:
查看答案和解析>>【题目】探究应用:用“∪”、“∩”定义两种新运算:对于两数a、b,规定a∪b=10a×10b,a∩b=10a÷10b,例如:3∪2=103×102=105,3∩2=103÷102=10.
(1) 求: (2017∪983) 的值
(2) 求: (2018∩2016) 的值;
(3) 当x为何值时, (x∪5)的值与 (23∩17)的值相等.
-
科目: 来源: 题型:
查看答案和解析>>【题目】某商场用24000元购入一批空调,然后以每台3000元的价格销售,因天气炎热,空调很快售完;商场又以52000元的价格再次购入该种型号的空调,数量是第一次购入的2倍,但购入的单价上调了200元,售价每台也上调了200元.
(1)商场第一次购入的空调每台进价是多少元?
(2)商场既要尽快售完第二次购入的空调,又要在这两次空调销售中获得的利润率不低于22%,打算将第二次购入的部分空调按每台九五折出售,最多可将多少台空调打折出售?
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,点C是线段AB上一点,△ACD和△BCE都是等边三角形,连结AE,BD,设AE交CD于点F.
(1)求证:△ACE≌△DCB;
(2)求证:△ADF∽△BAD.

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图:AB∥CD,直线l交AB、CD分别于点E、F,点M在EF上,N是直线CD上的一个动点(点N不与F重合)
(1)当点N在射线FC上运动时,∠FMN+∠FNM=∠AEF,说明理由;
(2)当点N在射线FD上运动时,∠FMN+∠FNM与∠AEF有什么关系并说明理由.

相关试题

