【题目】某校七年级400名学生到郊外参加植树活动,已知用3辆小客车和1辆大客车每次可运送学生105人,用1辆小客车和2辆大客车每次可运送学生110人.
(1)每辆小客车和每辆大客车各能坐多少名学生?
(2)若计划租小客车m辆,大客车n辆,一次送完,且恰好每辆车都坐满:
①请你设计出所有的租车方案;
②若小客车每辆租金150元,大客车每辆租金250元,请选出最省线的租车方案,并求出最少租金.
参考答案:
【答案】(1)每辆小客车能坐20人,每辆大客车能坐45人;
(2)①租车方案有三种:方案一:小客车20车、大客车0辆,方案二:小客车11辆,大客车4辆,方案三:小客车2辆,大客车8辆;
②最省钱的租车方案为方案三,租金最少为2300元.
【解析】试题分析:(1)设每辆小客车能坐x人,每辆大客车能坐y人,根据题意可得等量关系:3辆小客车座的人数+1辆大客车座的人数=105人;1辆小客车座的人数+2辆大客车座的人数=110人,根据等量关系列出方程组,再解即可;(2)①根据题意可得小客车m辆运的人数+大客车n辆运的人数=400,然后求出整数解即可;②根据①所得方案和小客车每辆租金150元,大客车每辆租金250元分别计算出租金即可.
试题解析:(1)设每辆小客车能坐x人,每辆大客车能坐y人,
据题意: ![]() ,
,
解得: ![]() ,
,
答:每辆小客车能坐20人,每辆大客车能坐45人;
(2)①由题意得:20m+45n=400,
∴n=![]() ,
,
∵m、n为非负整数,
∴![]() 或
或![]() 或
或![]() ,
,
∴租车方案有三种:
方案一:小客车20车、大客车0辆,
方案二:小客车11辆,大客车4辆,
方案三:小客车2辆,大客车8辆;
②方案一租金:150×20=3000(元),
方案二租金:150×11+250×4=2650(元),
方案三租金:150×2+250×8=2300(元),
-
科目: 来源: 题型:
查看答案和解析>>【题目】专家说:如果没有吃含三聚氰氨的奶粉,孩子得结石的几率很低。说明了这个事件( )
A.必然事件
B.不可能事件
C.不确定事件
D.以上说法均不对 -
科目: 来源: 题型:
查看答案和解析>>【题目】计算:aa2=
-
科目: 来源: 题型:
查看答案和解析>>【题目】将2×2的正方形网格如图放置在平面直角坐标系中,每个小正方形的顶点称为格点,每个小正方形的边长都是1,正方形ABCD的顶点都在格点上.若直线y=kx(k≠0)与正方形ABCD有公共点,则k的取值范围是( )
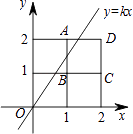
A.k≤2
B.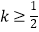
C.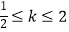
D.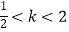
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,抛物线y=ax2+bx过A(4,0),B(1,3)两点,点C、B关于抛物线的对称轴对称,过点B作直线BH⊥x轴,交x轴于点H.
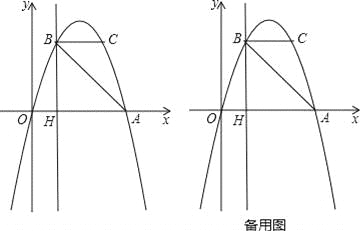
(1)求抛物线的表达式;
(2)直接写出点C的坐标,并求出△ABC的面积;
(3)点P是抛物线上一动点,且位于第四象限,当△ABP的面积为6时,求出点P的坐标;
(4)若点M在直线BH上运动,点N在x轴上运动,当以点C、M、N为顶点的三角形为等腰直角三角形时,请直接写出此时△CMN的面积.
-
科目: 来源: 题型:
查看答案和解析>>【题目】某网店打出促销广告:最潮新款服装30件,每件售价300元.若一次性购买不超过10件时,售价不变;若一次性购买超过10件时,每多买1件,所买的每件服装的售价均降低3元.已知该服装成本是每件200元,设顾客一次性购买服装x件时,该网店从中获利y元.
(1)求y与x的函数关系式,并写出自变量x的取值范围;
(2)顾客一次性购买多少件时,该网店从中获利最多?
-
科目: 来源: 题型:
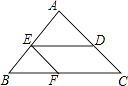
查看答案和解析>>【题目】如图,△ABC中,AB=AC,BC=12cm,点D在AC上,DC=4cm.将线段DC沿着CB的方向平移7cm得到线段EF,点E,F分别落在边AB,BC上,则△EBF的周长为cm.
相关试题

