搜索
【题目】已知反比例函数y= 
（k≠0）的图象经过点B（3，2），点B与点C关于原点O对称，BA⊥x轴于点A，CD⊥x轴于点D．
（1）求这个反比函数的解析式；
（2）求△ACD的面积．
参考答案：
【答案】
（1）
解：将B点坐标代入函数解析式，得
=2，
解得k=6，
∴反比例函数的解析式为y= 
；
（2）
解：由B（3，2），点B与点C关于原点O对称，得
C（﹣3，﹣2）．
由BA⊥x轴于点A，CD⊥x轴于点D，
得A（3，0），D（﹣3，0）．
∴S△ACD= 
ADCD= × [3﹣（﹣3）]×|﹣2|=6．
【解析】（1）根据待定系数法，可得函数解析式；
（2）根据三角形的面积公式，可得答案．
【考点精析】本题主要考查了三角形的面积和关于原点对称的点的坐标的相关知识点，需要掌握三角形的面积=1/2×底×高；两个点关于原点对称时，它们的坐标的符号相反，即点P（x，y）关于原点的对称点为P’（-x，-y）才能正确解答此题．
-
科目： 来源： 题型：
查看答案和解析>>【题目】阅读理解：用“十字相乘法”分解因式2x2﹣x﹣3的方法．
（i）二次项系数2=1×2；
（ii）常数项﹣3=﹣1×3=1×（﹣3），验算：“交叉相乘之和”；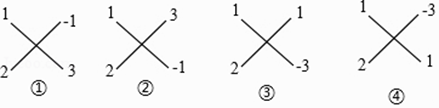
1×3+2×（﹣1）=1 1×（﹣1）+2×3=5 1×（﹣3）+2×1=﹣1 1×1+2×（﹣3）=﹣5
（iii）发现第③个“交叉相乘之和”的结果1×（﹣3）+2×1=﹣1，等于一次项系数﹣1．
即：（x+1）（2x﹣3）=2x2﹣3x+2x﹣3=2x2﹣x﹣3，则2x2﹣x﹣3=（x+1）（2x﹣3）．
像这样，通过十字交叉线帮助，把二次三项式分解因式的方法，叫做十字相乘法．仿照以上方法，分解因式：3x2+5x﹣12= ． -
科目： 来源： 题型：
查看答案和解析>>【题目】某电视台在它的娱乐性节目中每期抽出两名场外幸运观众，有一期甲、乙两人被抽为场外幸运观众，他们获得了一次抽奖的机会，在如图所示的翻奖牌的正面4个数字中任选一个，选中后翻开，可以得到该数字反面的奖品，第一个人选中的数字第二个人不能再选择了．
（1）如果甲先抽奖，那么甲获得“手机”的概率是多少？
（2）小亮同学说：甲先抽奖，乙后抽奖，甲、乙两人获得“手机”的概率不同，且甲获得“手机”的概率更大些．你同意小亮同学的说法吗？为什么？请用列表或画树状图分析． -
科目： 来源： 题型：
查看答案和解析>>【题目】如图，在等腰直角△ABC中，∠ACB=90°，点D为三角形内一点，且∠ACD=∠DAB=∠DBC．
（1）求∠CDB的度数；
（2）求证：△DCA∽△DAB；
（3）若CD的长为1，求AB的长． -
科目： 来源： 题型：
查看答案和解析>>【题目】矩形ABCD中，E、F分别是AD、BC的中点，CE、AF分别交BD于G、H两点．
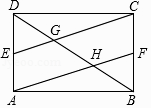
求证：
（1）四边形AFCE是平行四边形；
（2）证明：EG=FH． -
科目： 来源： 题型：
查看答案和解析>>【题目】甲、乙两运动员的射击成绩（靶心为10环）统计如下表（不完全）：
次数
运动员1
2
3
4
5
甲
10
8
9
10
8
乙
10
9
9
a
b
某同学计算出了甲的成绩平均数是9，方差是
S甲2=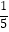
[（10﹣9）2+（8﹣9）2+（9﹣9）2+（10﹣9）2+（8﹣9）2]=0.8，请作答：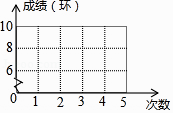
（1）在图中用折线统计图将甲运动员的成绩表示出来；
（2）若甲、乙射击成绩平均数都一样，则a+b=；
（3）在（2）的条件下，当甲比乙的成绩较稳定时，请列举出a、b的所有可能取值，并说明理由． -
科目： 来源： 题型：
查看答案和解析>>【题目】某校九年级10个班级师生举行毕业文艺汇演，每班2个节目，有歌唱与舞蹈两类节目，年级统计后发现唱歌类节目数比舞蹈类节目数的2倍少4个．
（1）九年级师生表演的歌唱与舞蹈类节目数各有多少个？
（2）该校七、八年级师生有小品节目参与，在歌唱、舞蹈、小品三类节目中，每个节目的演出平均用时分别是5分钟、6分钟、8分钟，预计所有演出节目交接用时共花15分钟，若从20：00开始，22：30之前演出结束，问参与的小品类节目最多能有多少个？
相关试题
