【题目】直角三角形ABC中,∠ACB=90°,直线l过点 C.
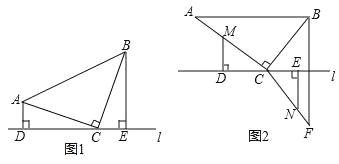
(1)当AC=BC时,如图1,分别过点A和B作AD⊥直线l于点D,BE⊥直线l于点 E.△ACD与△CBE是否全等,并说明理由;
(2)当AC=8cm,BC=6cm时,如图2,点B与点F关于直线l对称,连接BF、CF.点M是AC上一点,点N是CF上一点,分别过点M、N作MD⊥直线l于点D,NE⊥直线l于点E,点M从A点出发,以每秒1cm的速度沿A→C路径运动,终点为 C.点N从点F出发,以每秒3cm的速度沿F→C→B→C→F路径运动,终点为F.点M、N同时开始运动,各自达到相应的终点时停止运动,设运动时间为t秒.
①当△CMN为等腰直角三角形时,求t的值;
②当△MDC与△CEN全等时,求t的值.
参考答案:
【答案】(1)全等;证明见解析;(2)①3.5秒或5秒;②3.5秒或5秒或6.5秒.
【解析】
(1)根据垂直的定义得到∠DAC=∠ECB,利用AAS定理证明△ACD≌△CBE;
(2)①分点F沿C→B路径运动和点F沿B→C路径运动两种情况,根据等腰三角形的定义列出算式,计算即可;
②分点F沿F→C路径运动,点F沿C→B路径运动,点F沿B→C路径运动,点F沿C→F路径运动四种情况,根据全等三角形的判定定理列式计算.
解:(1)△ACD与△CBE全等.
理由如下:∵AD⊥直线l,
∴∠DAC+∠ACD=90°,
∵∠ACB=90°,
∴∠BCE+∠ACD=90°,
∴∠DAC=∠ECB,
在△ACD和△CBE中,
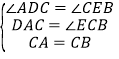 ,
,
∴△ACD≌△CBE(AAS);
(2)①由题意得,AM=t,FN=3t,
则CM=8﹣t,
由折叠的性质可知,CF=CB=6,
∴CN=6﹣3t,
点N在BC上时,△CMN为等腰直角三角形,
当点F沿C→B路径运动时,由题意得,8﹣t=3t﹣6,
解得,t=3.5,
当点F沿B→C路径运动时,由题意得,8﹣t=18﹣3t,
解得,t=5,
综上所述,当t=3.5秒或5秒时,△CMN为等腰直角三角形;
②由折叠的性质可知,∠BCE=∠FCE,
∵∠MCD+∠CMD=90°,∠MCD+∠BCE=90°,
∴∠NCE=∠CMD,
∴当CM=CN时,△MDC与△CEN全等,
当点F沿F→C路径运动时,8﹣t=6﹣3t,
解得,t=﹣1(不合题意),
当点F沿C→B路径运动时,8﹣t═3t﹣6,
解得,t=3.5,
当点F沿B→C路径运动时,由题意得,8﹣t=18﹣3t,
解得,t=5,
当点F沿C→F路径运动时,由题意得,8﹣t=3t﹣18,
解得,t=6.5,
综上所述,当t=3.5秒或5秒或6.5秒时,△MDC与△CEN全等.
-
科目: 来源: 题型:
查看答案和解析>>【题目】质地均匀的骰子六个面分别刻有1到6的点数,掷两次骰子,得到向上一面的两个点数,则下列事件中,发生可能性最大的是( )
A.点数都是偶数
B.点数的和为奇数
C.点数的和小于13
D.点数的和小于2 -
科目: 来源: 题型:
查看答案和解析>>【题目】从分别标有数﹣3,﹣2,﹣1,0,1,2,3的七张没有明显差别的卡片中,随机抽取一张,所抽卡片上的数的绝对值不小于2的概率是( )
A.
B.
C.
D.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,△ABC是一块绿化带,将阴影部分修建为花圃,已知AB=15,AC=9,BC=12,阴影部分是△ABC的内切圆,一只自由飞翔的小鸟将随机落在这块绿化带上,则小鸟落在花圃上的概率为( )
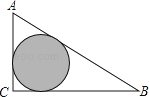
A.
B.
C.
D.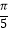
-
科目: 来源: 题型:
查看答案和解析>>【题目】下列算式
① =±3;②
=±3;②  =9;③26÷23=4;④
=9;③26÷23=4;④  =2016;⑤a+a=a2 .
=2016;⑤a+a=a2 .
运算结果正确的概率是( )
A.
B.
C.
D.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,随机地闭合开关S1 , S2 , S3 , S4 , S5中的三个,能够使灯泡L1 , L2同时发光的概率是 .

-
科目: 来源: 题型:
查看答案和解析>>【题目】任取不等式组
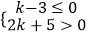 的一个整数解,则能使关于x的方程:2x+k=﹣1的解为非负数的概率为 .
的一个整数解,则能使关于x的方程:2x+k=﹣1的解为非负数的概率为 .
相关试题

