【题目】七年级(3)班学生参加学校组织的“绿色奥运”知识竞赛,老师将学生的成绩按10分的组距分段,统计每个分数段出现的频数,填入频数统计表,并绘制频数直方图.
七(3)班“绿色奥运”知识竞赛成绩频数统计表
分数段/分 | 组中值/分 | 频数/人 | 频率 |
49.5~59.5 | 54.5 | a | 0.050 |
59.5~69.5 | 64.5 | 9 | 0.225 |
69.5~79.5 | 74.5 | 10 | 0.250 |
79.5~89.5 | 84.5 | 14 | 0.350 |
89.5~99.5 | 94.5 | 5 | b |
七(3)班“绿色奥运”知识竞赛成绩频数直方图
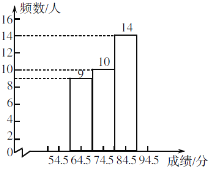
(1)频数统计表中a=_____,b=______;
(2)把频数直方图补充完整;
(3)学校设定成绩在69.5分以上的学生将获得一等奖或二等奖,一等奖奖励作业本15本及奖金50元,二等奖奖励作业本10本及奖金30元. 已知这部分学生共获得作业本335本,请你求出他们共获得的奖金.
参考答案:
【答案】(1)2;0.125;(2)直方图见解析;(3)他们共获得奖金1050元.
【解析】
先求出“89.5~99.5”分值的频率为1-0.050-0.225-0.250-0.350=0.125,再求出总人数5![]() 0.125=40(人),故a=40-9-10-14-5=2(人),则可补全直方图及解答.
0.125=40(人),故a=40-9-10-14-5=2(人),则可补全直方图及解答.
(1)2 ;0.125
(2)直方图如图所示
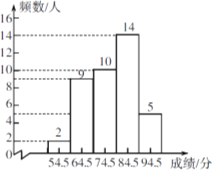
(3)设获得一等奖学生为x人,获得二等奖学生为y人,根据题意得![]() ,
,
解得![]() ,
,
9![]() 50+20
50+20![]() 30=1050元.
30=1050元.
答:他们共获得奖金1050元.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,∠ECF=90°,线段 AB 的端点分别在 CE 和 CF 上,BD 平分∠CBA,并与∠CAB 的外角平分线 AG 所在的直线交于一点 D.
(1)∠D 与∠C 有怎样的数量关系?(直接写出关系及大小)
(2)点 A 在射线 CE 上运动,(不与点 C 重合)时,其它条件不变,(1)中结论还成立吗?说说你的理由.

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,经过点A(0,6)的抛物线y=
 x2+bx+c与x轴相交于B(﹣2,0)、C两点.
x2+bx+c与x轴相交于B(﹣2,0)、C两点.
(1)求此抛物线的函数关系式和顶点D的坐标;
(2)求直线AC所对应的函数关系式;
(3)将(1)中求得的抛物线向左平移1个单位长度,再向上平移m(m>0)个单位长度得到新抛物线y1 , 若新抛物线y1的顶点P在△ABC内,求m的取值范围;
(4)在(3)的结论下,新抛物线y1上是否存在点Q,使得△QAB是以AB为底边的等腰三角形,请分析所有可能出现的情况,并直接写出相对应的m的取值范围. -
科目: 来源: 题型:
查看答案和解析>>【题目】在△ABC 中,BC=AC,∠BCA=90°,P 为直线 AC 上一点,过 A作 AD⊥BP 于 D,交直线 BC 于 Q.
(1)如图 1,当 P 在线段 AC 上时,求证:BP=AQ.
(2)当 P 在线段 AC 的延长线上时,请在图 2 中画出图形,并求∠CPQ.
(3)如图 3,当 P 在线段 AC 的延长线上时,∠DBA= 时,AQ=2BD.

-
科目: 来源: 题型:
查看答案和解析>>【题目】在一个不透明的袋子中,装有2个红球和1个白球,这些球除了颜色外都相同.如果第一次随机摸出一个小球(不放回),充分搅匀后,第二次再从剩余的两球中随机摸出一个小球,求两次都摸到红球的概率.(用树状图或列表法求解)
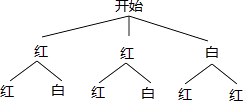
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图1,A(m,0),B(0,n),且m,n满足(m﹣2)2
 0.
0.(1)求S△ABO;
(2)点C为y轴负半轴上一点,BD⊥CA交CA的延长线于点D,若∠BAD=∠CAO,求
 的值;
的值;(3)点E为y轴负半轴上一点,OH⊥AE于H,HO,AB的延长线交于点F,G为y轴正半轴上一点,且BG=OE,FG,EA的延长线交于点P,求证:点P的纵坐标是定值.

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在数轴上有A,B,C,D,E五个整数点(即各点均表示整数),且AB=2BC=3CD=4DE,若A、E两点表示的数的分别为-13和12,那么,该数轴上上述五个点所表示的整数中,离线段AE的中点最近的整数是( )

A. -1 B. 5 C. 6 D. 8
相关试题

