【题目】(1)如图1,在AB直线一侧C、D两点,在AB上找一点P,使C、D、P三点组成的三角形的周长最短,找出此点并说明理由.
(2)如图2,在∠AOB内部有一点P,是否在OA、OB上分别存在点E、F,使得E、F、P三点组成的三角形的周长最短,找出E、F两点,并说明理由.
(3)如图3,在∠AOB内部有两点M、N,是否在OA、OB上分别存在点E、F,使得E、F、M、N,四点组成的四边形的周长最短,找出E、F两点,并说明理由.

参考答案:
【答案】(1)答案见解析;(2)答案见解析;(3)答案见解析.
【解析】
(1)由于△PCD的周长=PC+CD+PD,而CD是定值,故只需在直线l上找一点P,使PC+PD最小.如果设C关于l的对称点为C′,使PC+PD最小就是使PC′+PD最小;
(2)作P关于OA、OB的对称点C、D,连接CD角OA、OB于E、F.此时△PEF周长有最小值;
(3)如图3,作M关于OA的对称点C,关于OB的对称点D,连接CD,交OA于E,OB于F,此时使得E、F、M、N,四点组成的四边形的周长最短.
(1)如图1,作C关于直线AB的对称点C′,连接C′D交AB于点P.则点P就是所要求作的点.理由如下:
在l上取不同于P的点P′,连接CP′、DP′.
∵C和C′关于直线l对称,∴PC=PC′,P′C=P′C′,而C′P+DP<C′P′+DP′,∴PC+DP<CP′+DP′,∴CD+CP+DP<CD+CP′+DP′.即△CDP周长小于△CDP′周长;
(2)如图2,作P关于OA的对称点C,关于OB的对称点D,连接CD,交OA于E,OB于F,则点E,F就是所要求作的点,理由如下:
在OA,OB上取不同于E,F的点E′,F′.连接CE′、E′P、PF′、DF′.
∵C和P关于直线OA对称,∴PE=CE,CE′=PE′,PF=DF,PF′=DF′,∴PE+EF+PF=CE+EF+DF,PE′+PF′+E′F′=CE′+E′F′+DF′.
∵CE+EF+DF<CE′+E′F′+DF′,∴PE+EF+PF<PE′+E′F′+PF′;
(3)如图3,作M关于OA的对称点C,作N关于OB的对称点D,连接CD,交OA于E,OB于F,则点E,F就是所要求作的点.理由如下:
在OA,OB上取不同于E,F的点E′,F′,连接CE′、E′F′,DF′.
∵C和M关于直线OA对称,∴ME=CE,CE′=ME′,NF=DF,NF′=DF′,由(2)得知MN+ME+EF+NF<MN+ME′+E′F′+F′D.
-
科目: 来源: 题型:
查看答案和解析>>【题目】2016年5月27日,太原与大同之间开通了“点对点”的云冈号旅游列车(中间不停车),该列车为空调车,由6节硬座车厢、1节软卧车厢、1节硬卧车厢组成.行驶的路程约300km,该旅游列车从太原站出发,以平均速度110km/h开往大同.用x(h)表示列车行驶的时间,y(km)表示列车距大同的距离.
(1)写出y与x之间的函数关系式;
(2)当该旅游列车距大同就还有80km时,求行驶了多长时间.

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,点E正方形ABCD外一点,点F是线段AE上一点,△EBF是等腰直角三角形,其中∠EBF=90°,连接CE、CF.
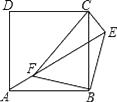
(1)求证:△ABF≌△CBE;
(2)判断△CEF的形状,并说明理由. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图1,直角坐标系中有一矩形OABC,其中O是坐标原点,点A,C分别在x轴和y轴上,点B的坐标为(3,4),直线y=
 x交AB于点D,点P是直线y=
x交AB于点D,点P是直线y=  x位于第一象限上的一点,连接PA,以PA为半径作⊙P,
x位于第一象限上的一点,连接PA,以PA为半径作⊙P, 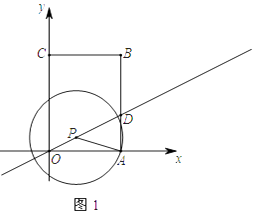
(1)连接AC,当点P落在AC上时,求PA的长;
(2)当⊙P经过点O时,求证:△PAD是等腰三角形;
(3)设点P的横坐标为m, ①在点P移动的过程中,当⊙P与矩形OABC某一边的交点恰为该边的中点时,求所有满足要求的m值;
②如图2,记⊙P与直线y= x的两个交点分别为E,F(点E在点P左下方),当DE,DF满足
x的两个交点分别为E,F(点E在点P左下方),当DE,DF满足  <
< 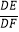 <3时,求m的取值范围.(请直接写出答案)
<3时,求m的取值范围.(请直接写出答案)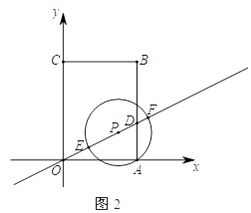
-
科目: 来源: 题型:
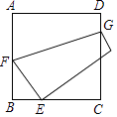
查看答案和解析>>【题目】如图,将正方形ABCD的一角折向边CD,使点A与CB上一点E重合,若BE=1,CE=2,则折痕FG的长度为( )
A.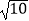
B.2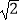
C.3
D.4 -
科目: 来源: 题型:
查看答案和解析>>【题目】如图:在长度为1个单位的小正方形组成的网格中,点A、B、C在小正方形的顶点上.
(1)在图中画出与△ABC关于直线l成轴对称的△AB′C′;
(2)△ABC的面积为________;
(3)在直线l上找一点P,使PB+PC的长最短,则这个最短长度为________个单位长度.(在图形中标出点P)

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,矩形OABC的顶点A,C分别在x轴和y轴上,点B的坐标为(4,6).双曲线y=
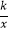 (x>0)的图象经过BC的中点D,且与AB交于点E,连接DE.
(x>0)的图象经过BC的中点D,且与AB交于点E,连接DE.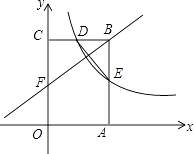
(1)求k的值及点E的坐标;
(2)若点F是边上一点,且△BCF∽△EBD,求直线FB的解析式.
相关试题

