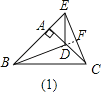
【题目】如图,在△ABC和△ADE中,AB=AC,AD=AE,∠BAC=∠DAE=90°.

①当点D在AC上时,如图(1),线段BD、CE有怎样的数量关系和位置关系?直接写出你猜想的结论;
②将图(1)中的△ADE的位置改变一下,如图(2),使∠BAD=∠CAE,其他条件不变,则线段BD,CE又有怎样的数量关系和位置关系?请说明理由.
参考答案:
【答案】①BD=CE,BD⊥CE;②BD=CE,BD⊥CE,理由见解析
【解析】
试题分析:(1)BD=CE,BD⊥CE,延长BD与EC交于点F,可以证明△ACE≌△ADB,可得BD=CE,且∠BFE=90°,即可解答;
(2)BD=CE,BD⊥CE,延长BD交AC于F,交CE于H,可以证明△ACE≌△ADB,可得BD=CE,利用三角形的内角和为180°,即可得到BD⊥CE.
解:(1)BD=CE,BD⊥CE;
如图(1),延长BD与EC交于点F,
在△ACE和△ADB中,
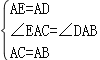 ,
,
∴△ACE≌△ADB(SAS),
∴BD=CE,∠AEC=∠ADB,
∵∠ADB+∠ABD=90°
∴∠ABD+∠AEC=90°
∴∠BFE=90°,
∴BD⊥CE.
(2)结论:BD=CE,BD⊥CE,
理由如下:∵∠BAC=∠DAE=90°
∴∠BAC﹣∠DAC=∠DAE﹣∠DAC,
即∠BAD=∠CAE,
在△ABD与△ACE中,
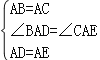
∴△ABD≌△ACE(SAS)
∴BD=CE,
如图(2),延长BD交AC于F,交CE于H.

在△ABF与△HCF中,
∵∠ABF=∠HCF,∠AFB=∠HFC
∴∠CHF=∠BAF=90°
∴BD⊥CE.
-
科目: 来源: 题型:
查看答案和解析>>【题目】下列说法中,正确的是( )
A.同位角相等
B.矩形的对角线一定互相垂直
C.对角线相等的四边形是矩形
D.四条边相等的四边形是菱形 -
科目: 来源: 题型:
查看答案和解析>>【题目】某商场在“五一”期间举行促销活动,根据顾客按商品标价一次性购物总额,规定相应的优惠方法:①如果不超过500元,则不予优惠;②如果超过500元,但不超过800元,则按购物总额给予8折优惠;③如果超过800元,则其中800元给予8折优惠,超过800元的部分给予6折优惠.促销期间,小红和她母亲分别看中一件商品,若各自单独付款,则应分别付款480元和520元;若合并付款,则她们总共只需付款多少元 ( )
A.838
B.924
C.924或838
D.838或910 -
科目: 来源: 题型:
查看答案和解析>>【题目】某校学生利用双休时间去距学校10km的炎帝故里参观,一部分学生骑自行车先走,过了20min后,其余学生乘汽车沿相同路线出发,结果他们同时到达。已知汽车的速度是骑车学生速度的2倍,求骑车学生的速度和汽车的速度.
-
科目: 来源: 题型:
查看答案和解析>>【题目】点P(﹣2,3)关于y轴对称的点的坐标是( )
A. (2,3) B. (﹣2,3) C. (2,﹣3) D. (﹣2,﹣3)
-
科目: 来源: 题型:
查看答案和解析>>【题目】计算:(﹣3a2b3)2= .
-
科目: 来源: 题型:
查看答案和解析>>【题目】解方程:
(1)4(2x﹣3)﹣(5x﹣1)=7
(2)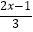 ﹣
﹣ 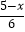 =﹣2
=﹣2
(3)2x﹣ [x﹣
[x﹣  (x﹣1)]=
(x﹣1)]=  (x﹣1)
(x﹣1)
(4)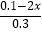 =1+
=1+ 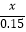 .
.
相关试题

