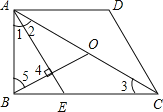
【题目】如图,在四边形ABCD中,∠ABC=90°,AD∥BC,AE∥CD交BC于点E,AE平分∠BAC,AO=CO,AD=DC=2,下面结论:①AC=2AB;②AB=![]() ;③S△ADC=2S△ABE;④BO⊥AE.其中正确的有( )
;③S△ADC=2S△ABE;④BO⊥AE.其中正确的有( )
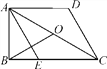
A. 1个 B. 2个 C. 3个 D. 4个
参考答案:
【答案】D
【解析】试题分析:∵AD∥BC,AE∥CD,
∴四边形AECD是平行四边形.
∵AD=DC,
∴四边形AECD是菱形,
∴AE=EC=CD=AD=2,
∴∠2=∠3.
∵∠1=∠2,
∴∠1=∠2=∠3.
∵∠ABC=90°,
∴∠1+∠2+∠3=90°,
∴∠1=∠2=∠3=30°,
∴BE=![]() AE=1,AC=2AB.①正确;
AE=1,AC=2AB.①正确;
在Rt△ABE中,由勾股定理,得
AB=![]() =
=![]() =
=![]() ,②正确;
,②正确;
∵O是AC的中点,∠ABC=90°,
∴BO=AO=CO=![]() AC.
AC.
∵∠1=∠2=∠3=30°,
∴∠BAO=60°,
∴△ABO为等边三角形.
∵∠1=∠2,
∴AE⊥BO.④正确;
∵S△ADC=S△AEC=![]() AB·CE ,S△ABE=
AB·CE ,S△ABE=![]() AB·BE,
AB·BE,
∵CE=2,BE=1,
∴CE=2BE,
∴S△ACE=![]() AB·2BE
AB·2BE
=2×![]() AB·BE ,
AB·BE ,
∴S△ACE=2S△ABE,
∴S△ADC=2S△ABE.③正确.
∴正确的个数有4个.
故选D.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知AB⊥BC,BC⊥CD,∠1=∠2.试判断BE与CF的关系,并说明你的理由.
解:BE∥CF.
理由:∵AB⊥BC,BC⊥CD(已知)
∴∠ =∠ =90°( )
∵∠1=∠2( )
∴∠ABC﹣∠1=∠BCD﹣∠2,即∠EBC=∠BCF.
∴ ∥ .(____________,______________)

-
科目: 来源: 题型:
查看答案和解析>>【题目】下列说法:①经过两点有且只有一条直线;②直线比射线长;③两点之间的所有连线中直线最短;④连接两点的线段叫两点之间的距离;其中正确的有( )
A.0个B.1个C.2个D.3个
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,EF∥AD,AD∥BC,CE平分∠BCF,∠DAC=115°,∠ACF=25°,求∠FEC的度数.

-
科目: 来源: 题型:
查看答案和解析>>【题目】已知(m+n)2=9, (m-n)2=4.求
(1)m2n2的值
(2)m2+n2的值
-
科目: 来源: 题型:
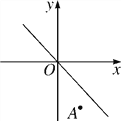
查看答案和解析>>【题目】如图,将直线y=-x沿y轴向下平移后的直线恰好经过点A(2,-4),且与y轴交于点B,在x轴上存在一点P使得PA+PB的值最小,则点P的坐标为________.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图所示,在菱形ABCD中,AB=4,∠BAD=120°,△AEF为正三角形,点E、F分别在菱形的边BC、CD上滑动,且E、F不与B、C、D重合.当点E、F在BC、CD上滑动时,则△CEF的面积最大值是____.

相关试题

