【题目】某数学兴趣小组在学习了《锐角三角函数》以后,开展测量物体高度的实践活动,测量一建筑物CD的高度,他们站在B处仰望楼顶C,测得仰角为30°,再往建筑物方向走20m,到达点F处测得楼顶C的仰角为45°(BFD在同一直线上).已知观测员的眼睛与地面距离为1.5m(即AB=1.5m),求这栋建筑物CD的高度.(参考数据: ![]() ≈1.732,
≈1.732, ![]() ≈1.414.结果保留整数)
≈1.414.结果保留整数)
参考答案:
【答案】解:延长AE交CD于点G.设CG=xm,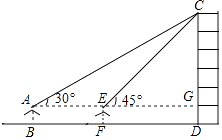
在直角△CGE中,∠CEG=45°,则EG=CG=xm.
在直角△ACG中,AG= ![]() =
= ![]() xm.
xm.
∵AG﹣EG=AE,
∴ ![]() x﹣x=20,
x﹣x=20,
解得:x=10( ![]() +1)≈27.32.
+1)≈27.32.
则CD=27.32+1.5=28.82≈29(m)
【解析】延长AE交CD于点G.设CG=xm,根据∠CEG=45°可知EG=CG=xm,在直角△ACG中,利用锐角三角函数的定义可得出x的值,进而得出结论.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知△ABC和△DEC都是等腰直角三角形,C为它们的公共直角顶点,D、E分别在BC、AC边上.
(1)如图1,F是线段AD上的一点,连接CF,若AF=CF;
①求证:点F是AD的中点;
②判断BE与CF的数量关系和位置关系,并说明理由;
(2)如图2,把△DEC绕点C顺时针旋转α角(0<α<90°),点F是AD的中点,其他条件不变,判断BE与CF的关系是否不变?若不变,请说明理由;若要变,请求出相应的正确结论.

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,所有正方形的中心均在坐标原点,且各边与x轴或y轴平行,从内到外,它们的边长依次为2,4,6,8,…顶点依次用A1,A2,A3,A4表示,则顶点A2018的坐标是( )
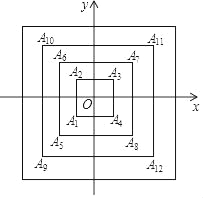
A. (504,﹣504) B. (﹣504,504) C. (505,﹣505) D. (﹣505,505)
-
科目: 来源: 题型:
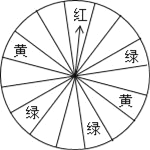
查看答案和解析>>【题目】“六一”儿童节期间,某商厦为了吸引顾客,设立了一个可以自由转动的转盘(转盘被平均分成16份),并规定:顾客每购买100元的商品,就能获得一次转动转盘的机会.如果转盘停止后,指针正好对准哪个区域,顾客就可以获得相应的奖品.
颜色
奖品
红色
玩具熊
黄色
童话书
绿色
彩笔
小明和妈妈购买了125元的商品,请你分析计算:
(1)小明获得奖品的概率是多少?
(2)小明获得童话书的概率是多少?
-
科目: 来源: 题型:
查看答案和解析>>【题目】请把下列各数填入相应的集合中.
2,0,2π,
 ,2018,﹣0.030030003…
,2018,﹣0.030030003…有理数集合:{___________________________________________…};
无理数集合:{___________________________________________…};
非负整数集合:{_________________________________________…}.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在平面直角坐标系中有一个轴对称图形,A(3,-2),B(3,﹣6)两点在此图形上且互为对称点,若此图形上有一个点C(﹣2,+1).
(1)求点C的对称点的坐标.
(2)求△ABC的面积.

-
科目: 来源: 题型:
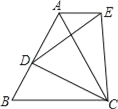
查看答案和解析>>【题目】如图,等边△ABC中,D是AB边上的一动点,以CD为一边,向上作等边△EDC,连接AE.
(1)求证:△ACE≌△BCD;
(2)判断AE与BC的位置关系,并说明理由.
相关试题

