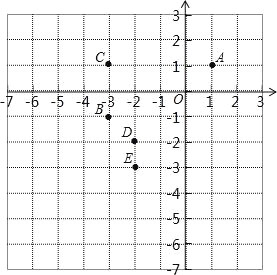
【题目】在同一平面直角坐标系中有6个点:
A(1,1),B(﹣3,﹣1),C(﹣3,1),D(﹣2,﹣2),E(﹣2,﹣3),F(0,﹣4).
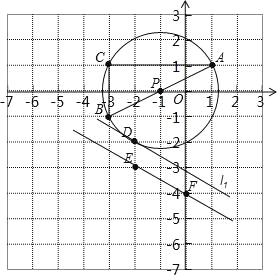
(1)画出△ABC的外接圆⊙P,则点D与⊙P的位置关系 ;
(2)△ABC的外接圆的半径= ,△ABC的内切圆的半径= .
(3)若将直线EF沿y轴向上平移,当它经过点D时,设此时的直线为l1.判断直线l1与⊙P的位置关系,并说明理由.
参考答案:
【答案】(1)点在圆上
(2)![]() ,3﹣
,3﹣![]() ;
;
(3)直线l1与⊙P相交.
【解析】
试题分析:(1)分别找出AC与BC的垂直平分线,交于点P,即为圆心,求出AP的长即为圆的半径,画出圆P,如图所示,求出D到圆心P的距离,与半径比较即可做出判断;
(2)求出三角形ABC的外接圆半径,内切圆半径即可;
(3)利用待定系数法求出直线EF的解析式,利用平移性质及题意确定出直线l1解析式,求出圆心P到l1的距离d,与半径r比较,即可得出直线与圆的位置关系.
试题解析:(1)画出△ABC的外接圆⊙P,如图所示,
∵DP=![]() =
=![]() =r,
=r,
∴点D与⊙P的位置关系是点在圆上;
(2)△ABC的外接圆的半径=![]() ,△ABC的内切圆的半径=
,△ABC的内切圆的半径=![]() ;
;
(3)设直线EF解析式为y=kx+b,
把E和F坐标代入得:![]() ,
,
解得:k=﹣![]() ,b=﹣4,
,b=﹣4,
∴直线EF解析式为y=﹣![]() x﹣4,
x﹣4,
由平移性质及题意得:直线l1解析式为y+2=﹣![]() (x+2),即x+2y+6=0,
(x+2),即x+2y+6=0,
∵圆心P(0,﹣1)到直线的距离d=![]() <
<![]() =r,
=r,
∴直线l1与⊙P相交.
故答案为:(1)点在圆上;(2)![]() ;3﹣
;3﹣![]()
-
科目: 来源: 题型:
查看答案和解析>>【题目】下列单项式中,与a2b是同类项的是( )
A. ab2 B. 2a2b C. a2b2 D. 3ab
-
科目: 来源: 题型:
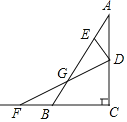
查看答案和解析>>【题目】如图,Rt△ABC中,∠C=90°,∠A=30°,点D,E分别在边AC,AB上,点D与点A,点C都不重合,点F在边CB的延长线上,且AE=ED=BF,连接DF交AB于点G.若BC=4,则线段EG的长为__________.
-
科目: 来源: 题型:
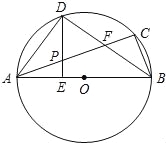
查看答案和解析>>【题目】已知:如图,△ABC内接于⊙O,AB为直径,∠CBA的平分线交AC于点F,交⊙O于点D,DE⊥AB于点E,且交AC于点P,连结AD.
(1)求证:∠DAC=∠DBA;
(2)求证:P是线段AF的中点;
(3)连接CD,若CD﹦3,BD﹦4,求⊙O的半径和DE的长.
-
科目: 来源: 题型:
查看答案和解析>>【题目】分解因式:a3﹣16a= .
-
科目: 来源: 题型:
查看答案和解析>>【题目】一种零件的内径尺寸在图纸上是50±0.05(单位:mm),表示这种零件的内径标准尺寸是多少?加工要求最大不超过标准尺寸多少毫米?符合要求的零件内径最小是多少毫米?
-
科目: 来源: 题型:
查看答案和解析>>【题目】H7N9禽流感病毒的直径大约为0.0000000805米,这个数用科学记数法表示为( )
A.8.05×10﹣8
B.8.05×10﹣7
C.80.5×10﹣9
D.0.805×10﹣7
相关试题

