【题目】如图1所示,△ABC中,AD⊥BC,AE平分∠BAC.
(1)若∠B=30°,∠C=70°,求∠DAE的度数,并说明理由;
(2)若∠B=α,∠C=β(α<β),请你根据(1)问的结果大胆猜想∠DAE与α,β间的等量关系.

参考答案:
【答案】(1)20°;(2)∠DAE=![]() .
.
【解析】
(1)首先根据三角形的内角和定理,求出∠BAC的度数;然后根据角平分线的性质,求出∠BAE、∠CAE的度数是多少;最后根据三角形的外角的性质,求出∠AED的度数,进而求出∠DAE的度数是多少即可.
(2)根据(1)问的结果,猜想∠DAE与α,β间的等量关系为:∠DAE![]() ,然后根据(1)中求解的方法,证明猜想的正确性即可.
,然后根据(1)中求解的方法,证明猜想的正确性即可.
(1)∵∠B=30°,∠C=70°,∴∠BAC=180°﹣30°﹣70°=80°.
∵AE平分∠BAC,∴∠BAE=∠CAE=80°÷2=40°.
∵∠AED=∠B+∠BAE=30°+40°=70°,∴∠DAE=90°﹣70°=20°.
(2)根据(1)问的结果,猜想∠DAE与α,β间的等量关系为:∠DAE![]() .证明如下:
.证明如下:
∵∠B=α,∠C=β,∴∠BAC=180°﹣α﹣β.
∵AE平分∠BAC,∴∠BAE=∠CAE=(180°﹣α﹣β)÷2=90°![]() .
.
∵∠AED=∠B+∠BAE=α+(90°![]() )=90°
)=90°![]() ,∴∠DAE=90°﹣(90°
,∴∠DAE=90°﹣(90°![]() .
.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在Rt△ABC中,D,E为斜边AB上的两个点,且BD=BC,AE=AC,则∠DCE的大小为(度).
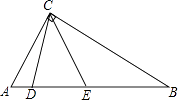
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知:如图,∠MON=40°,OE平分∠MON,A,B,C分别是射线OM,OE,ON上的动点(A,B,C不与点O 重合),连接AC交射线OE于点D.设∠OAC=x°.
(1)如图①,若AB∥ON,则
①∠ABO的度数是________.
②当∠BAD=∠ABD时,x=________;当∠BAD=∠BDA时,x=________.
(2)如图②,若AB⊥OM,则是否存在这样的x值,使得△ADB中有两个相等的角?若存在,求出x的值;若不存在,说明理由.

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在△ABC中,∠BAC的平分线与BC边的垂直平分线相交于点P,过点P作AB、AC(或延长线)的垂线,垂足分别是M、N,求证:BM=CN.
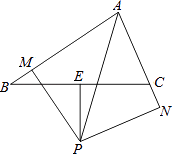
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,点C为线段AB上一点,△ACM,△CBN是等边三角形,直线AN,MC交于点E,直线BM,CN交于点F.

(1)求证:AN=MB;
(2)求证:△CEF为等边三角形;
(3)将△ACM绕点C按逆时针方向旋转90°,其他条件不变,在(2)中画出符合要求的图形,并判断(1)(2)题中的两结论是否依然成立.并说明理由. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在△ABC中,将△ABC在平面内绕点A逆时针旋转50角后得到△AB′C′的位置,若此时恰有CC′∥AB,则∠CAB′的度数为( )

A.15°
B.40°
C.50°
D.65° -
科目: 来源: 题型:
查看答案和解析>>【题目】如图:在正方形网格中有一个△ABC,按要求进行下列作图(只能借助于网格).
(1)画出△ABC中BC边上的高AH和BC边上的中线AD.
(2)画出将△ABC向右平移5格又向上平移3格后的△A′B′C′.
(3)△ABC的面积为 .
(4)若连接AA′,CC′,则这两条线段之间的关系是 .

相关试题

