【题目】几何知识可以解决生活中许多距离最短的问题.让我们从书本一道习题入手进行知识探索.
【回忆】
如图,A、B是河l两侧的两个村庄.现要在河l上修建一个抽水站C,使它到A、B两村庄的距离的和最小,请在图中画出点C的位置,并说明理由.
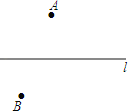
【探索】
(1)如图,A、B两个村庄在一条笔直的马路的两端,村庄 C在马路外,要在马路上建一个垃圾站O,使得AO+BO+CO最小,请在图中画出点O的位置,并说明理由.

(2)如图,A、B、C、D四个村庄,现建一个垃圾站O,使得AO+BO+CO+DO最小,请在图中画出点O的位置,并说明理由.
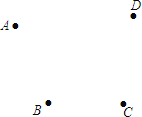
参考答案:
【答案】(1)见解析;(2)见解析
【解析】
试题分析:【回忆】根据两点之间线段最短即可确定;
【探索】(1)根据垂线段最短即可解答;
(2)根据两点之间线段最短即可解答.
解:【回忆】如图所示:

理由:两点之间线段最短;
【探索】
(1)如图所示:
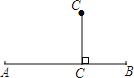
理由:点到直线的距离垂线段最短;
(2)如图所示:
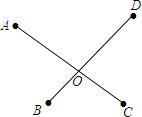
理由:两点之间线段最短(到OA、OC最短在AC上;到OB、OD最短在BD上).
-
科目: 来源: 题型:
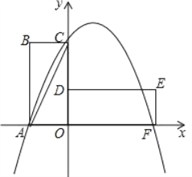
查看答案和解析>>【题目】如图,在平面直角坐标系中,矩形OABC的边OA在x轴的负半轴上,边OC在y轴的正半轴上,且OA=1,tan∠ACB=2,将矩形OABC绕点O按顺时针方向旋转90°后得到矩形ODEF.点A的对应点为点D,点B的对应点为点E,点C的对应点为点F,抛物线y=ax2+bx+2的图象过点A,C,F.
(1)求抛物线所对应函数的表达式;
(2)在边DE上是否存在一点M,使得以O,D,M为顶点的三角形与△ODE相似,若存在,求出经过M点的反比例函数的表达式,若不存在,请说明理由;
(3)在x轴的上方是否存在点P,Q,使以O,F,P,Q为顶点的平行四边形的面积是矩形OABC面积的2倍,且点P在抛物线上,若存在,请求出P,Q两点的坐标;若不能存在,请说明理由;
(4)在抛物线的对称轴上是否存在一点H,使得HA﹣HC的值最大,若存在,直接写出点H的坐标;若不存在,请说明理由.
-
科目: 来源: 题型:
查看答案和解析>>【题目】在体育课上,九年级2名学生各练习10次立定跳远,要判断哪一名学生的成绩比较稳定,通常需要比较这2名学生立定跳远成绩的( )
A.方差B.平均数C.频率分布D.众数
-
科目: 来源: 题型:
查看答案和解析>>【题目】计算:-48 x3y2÷6x2y=__________
-
科目: 来源: 题型:
查看答案和解析>>【题目】若m,n互为相反数,则m2+2mn+n2=_____
-
科目: 来源: 题型:
查看答案和解析>>【题目】计算:
(1)(2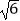 +3
+3 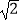 )(2
)(2 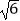 ﹣3
﹣3 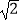 )
)
(2)(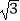 ﹣1)2﹣(3﹣
﹣1)2﹣(3﹣ 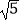 )(3+
)(3+ 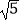 )
)
(3)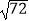 ÷3
÷3 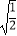 ×
× 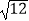
(4)(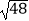 +
+ 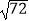 ﹣
﹣ 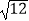 )÷(
)÷( 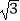 ×
× 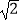 )
) -
科目: 来源: 题型:
查看答案和解析>>【题目】如图1,点O为直线AB上一点,过点O作射线OC,使∠AOC=60°,将一把直角三角尺的直角顶点放在点O处,一边OM在射线OB上,另一边ON在直线AB的下方.
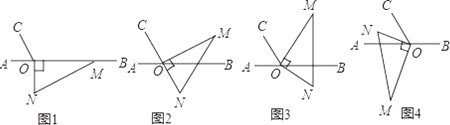
(1)将图1中的三角尺绕点O逆时针旋转至图2,使点N在OC的反向延长线上,请直接写出图中∠MOB的度数,∠MOB= .
(2)将图1中的三角尺绕点O逆时针旋转至图3,使一边OM在∠BOC的内部,且恰好平分∠BOC,求∠CON的度数.
(3)将图1中的三角尺绕点O顺时针旋转至图4,使ON在∠AOC的内部,请探究∠AOM与∠NOC之间的数量关系,并说明理由.
(4)将图1中的三角尺绕点O以每秒钟15°的转速顺时针旋转一周,当时间t为 秒钟时,ON所在的直线恰好平分∠AOC.(直接写答案)
相关试题

