搜索
【题目】如图，在梯形ABCD中，已知AD∥BC，AB=CD，延长线段CB到E，使BE=AD，连接AE、AC.
【1】求证：△ABE≌△CDA；
【2】若∠DAC=40°，求∠EAC的度数.
参考答案：
【答案】
【1】见解析
【2】100°
【解析】⑴利用SAS求证△ABE≌△CDA
⑵利用△ABE≌△CDA和平行线的性质以及等腰三角形的性质求解
⑴证明：在梯形ABCD中，∵AD∥BC，AB=CD，
∴∠ABE=∠BAD，∠BAD=∠CDA.
∴∠ABE=∠CDA.
在△ABE和△CDA中，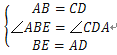
∴△ABE≌△CDA.
⑵解：由⑴得：∠AEB=∠CAD，AE=AC.
∴∠AEB=∠ACE.
]∵∠DAC=40°∴∠AEB=∠ACE=40°.
∴∠EAC=180°－40°－40°=100°.
-
科目： 来源： 题型：
查看答案和解析>>【题目】如图，直角梯形ABCD中，AD∥BC，AB⊥BC，AD＝2，将腰CD以D为中心逆时针旋转90°至DE，连接AE、CE，△ADE的面积为3，则BC的长为____________．
-
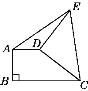
科目： 来源： 题型：
查看答案和解析>>【题目】已知：如图，二次函数y=ax2+bx+c的图象与x轴交于A、B两点，其中A点坐标为（﹣1，0），点C（0，5），另抛物线经过点（1，8），M为它的顶点．
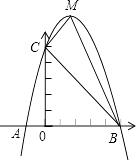
（1）求抛物线的解析式；
（2）求△MCB的面积S△MCB ． -
科目： 来源： 题型：
查看答案和解析>>【题目】（1）如图（1），已知：在△ABC中，∠BAC＝90°，AB=AC，直线m经过点A，BD⊥直线m, CE⊥直线m,垂足分别为点D、E.证明:DE=BD+CE.
（2） 如图（2），将（1）中的条件改为：在△ABC中，AB=AC，D、A、E三点都在直线m上,并且有∠BDA=∠AEC=∠BAC=
,其中为任意锐角或钝角.请问结论DE=BD+CE是否成立?如成立,请你给出证明;若不成立,请说明理由.（3）拓展与应用：如图（3），D、E是D、A、E三点所在直线m上的两动点（D、A、E三点互不重合）,点F为∠BAC平分线上的一点,且△ABF和△ACF均为等边三角形，连接BD、CE,若∠BDA=∠AEC=∠BAC，试判断△DEF的形状.
-
科目： 来源： 题型：
查看答案和解析>>【题目】如图，在Rt△ABC中，∠ACB＝90°，点D，F分别在AB，AC上，CF＝CB．连接CD，将线段CD绕点C按顺时针方向旋转90°后得CE，连接EF．
（1）求证：△BCD≌△FCE；
（2）若EF∥CD．求∠BDC的度数．
-
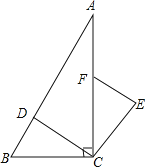
科目： 来源： 题型：
查看答案和解析>>【题目】如图，在△ABC中，AD是BC上的高，tanB=cos∠DAC．
（1）求证：AC=BD；
（2）若sin∠C=
，BC=12，求AD的长． -
科目： 来源： 题型：
查看答案和解析>>【题目】如图，在△AEC和△DFB中，∠E＝∠F，点A，B，C，D在同一直线上，有如下三个关系式：①AE∥DF，②AB＝CD，③CE＝BF.
(1)请用其中两个关系式作为条件，另一个作为结论，写出你认为正确的所有命题(用序号写出命题书写形式：“如果，，那么”)；
(2)选择(1)中你写出的一个命题，说明它正确的理由．
相关试题
