【题目】如图,已知函数y=x+1的图象与y轴交于点A,一次函数y=kx+b的图象经过点B(0,-1),与x轴以及y=x+1的图象分别交于点C、D,且点D的坐标为(1,n),

(1)点A的坐标是 ,n= ,k= ,b= ;
(2)x取何值时,函数y=kx+b的函数值大于函数y=x+1的函数值;
(3)求四边形AOCD的面积;
(4)是否存在y轴上的点P,使得以点P,B,D为顶点的三角形是等腰三角形?若存在求出点P的坐标;若不存在,请说明理由.
参考答案:
【答案】(1)(0,1),2,3,-1;(2)x>1;(3)![]() ;(4)(0,5),(0,-1-
;(4)(0,5),(0,-1-![]() ),P(0,
),P(0, ![]() -1)或(0,
-1)或(0, ![]() ).
).
【解析】试题分析:(1)由函数y=x+1的图象与y轴交于点A,可求点A的坐标,由y=x+1的图象过点D,且点D的坐标为(1,n),可得D的坐标,由一次函数y=kx+b的图象经过点B(0,-1)与D(1,2),即可求出k,b的值.
(2)根据图象即可得出答案;
(3)先求出点D的坐标,再求出BD的解析式,然后根据S四边形AOCD=S△AOD+S△COD即可求解;
(4)分三种情况讨论:①当DP=DB时,②当BP=DB时,③当PB=PD时分别求解.
试题解析:(1)∵函数y=x+1的图象与y轴交于点A,
∴令x=0时,y=0+1,解得y=1,
∴A(0,1),
∵y=x+1的图象过点D,且点D的坐标为(1,n),
∴n=1+1=2,
∴D(1,2),
∵一次函数y=kx+b的图象经过点B(0,-1)与D(1,2),
∴![]() 解得
解得![]() ,
,
∴一次函数的表达式为y=3x-1
(2)由一次函数图象可得当x>1时,函数y=kx+b的函数值大于函数y=x+1的函数值;
(3)∵D(1,2),
∴直线BD的解析式为y=3x-1,
∴A(0,1),C(![]() ,0)
,0)
∴S四边形AOCD=S△AOD+S△COD=![]() ×1×1+
×1×1+![]() ×
×![]() ×2=
×2=![]()
(4)①当DP=DB时,设P(0,y),
∵B(0,-1),D(1,2),
∴DP2=12+(y-2)2=DB2=12+(2+1)2,
∴P(0,5);
②当BP=DB时,DB=![]() ,∴P(0,-1-
,∴P(0,-1-![]() )或P(0,
)或P(0, ![]() -1);
-1);
③当PB=PD时,设P(0,a),则(a+1)2=1+(2-a)2,解得a=![]() ,
,
∴P(0, ![]() ).
).
综上所述点P的坐标为(0,5),(0,-1-![]() ),P(0,
),P(0, ![]() -1)或(0,
-1)或(0, ![]() ).
).
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图.矩形纸片ABCD中,已知AD=8,折叠纸片使AB边与对角线AC重合,点B落在点F处,折痕为AE,且EF=3.则AB的长为( )
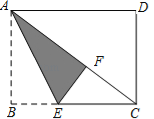
A. 3 B. 4 C. 5 D. 6
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,是一次函数y=kx+b的图象.
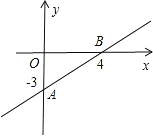
(1)求这个一次函数的解析式?
(2)试判断点P(1,-1)是否在这个一次函数的图象上?
(3)求原点O到直线AB的距离.
-
科目: 来源: 题型:
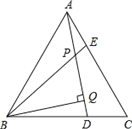
查看答案和解析>>【题目】如图,△ABC是等边三角形,AE=CD,BQ⊥AD于Q,BE交AD于P.
(1)求证:△ABE≌△CAD;
(2)求∠PBQ的度数.
-
科目: 来源: 题型:
查看答案和解析>>【题目】若a<0<b,则化简|a-b|+a的结果为__________.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图:已知正方形的边长为4,甲、乙两动点分别从正方形ABCD的顶点
A. C同时沿正方形的边开始移动,甲点依顺时针方向环行,乙点依逆时针方向环行,若乙的速度是甲的速度的3倍,则它们第2017次相遇在边 ( )上.
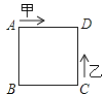
A.AB
B. BC
C. CD
D. DA
-
科目: 来源: 题型:
查看答案和解析>>【题目】一艘船从甲码头到乙码头顺流行驶,用了2个小时,从乙码头返回甲码头逆流行驶,用了2.5小时,已知水流的速度是3千米/时,则船在静水中的速度是_____千米/时.
相关试题

