搜索
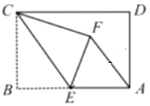
【题目】矩形ABCD中，AB=4，BC=3，点E为AB的中点，将矩形ABCD沿CE折叠，使得点B落到点F的位置.
(1)求证：AF∥CE.
(2)求AF的长度.
参考答案：
【答案】（1）见解析；（2）
.
【解析】
（1）由折叠性质可得
，BE=EF，由E为AB的中点可得EF=EA即可得出
，根据外角性质可得
，由
即可证明
，根据平行线的判定定理即可得答案；（2）过E作EG⊥AF，利用勾股定理求出CE的长，由（1）可知，即可得ΔCBE∽ΔEGA，根据相似三角形的性质可求出AG的长，根据AF=2AG即可得答案.
（1）∵ΔCBE沿CE折叠，
∴，BE=EF，
∵E是AB的中点，
∴EF=EA，
∴，
又∵，，
∴，
∴AF∥CE.
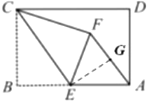
(2)过E作EG⊥AF
∴
∵四边形ABCD是矩形
∴
在RtΔCBE中
∵
由（1）可知，
∴ΔCBE∽ΔEGA
∴
即
∴
∴
-
科目： 来源： 题型：
查看答案和解析>>【题目】如图，在平面直角坐标系中，正方形ABCD与正方形BEFG是以原点O为位似中心的位似图形，且相似比为
，点A，B，E在x轴上，若正方形BEFG的边长为6，则点C的坐标为（ ）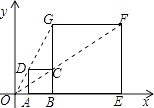
A.（2，2）
B.（3，1）
C.（3，2）
D.（4，2） -
科目： 来源： 题型：
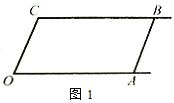
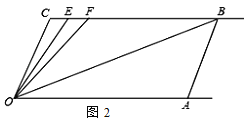
查看答案和解析>>【题目】如图1，已知射线CB∥OA，∠C=∠OAB，
（1）求证：AB∥OC；
（2）如图2，E、F在CB上，且满足∠FOB=∠AOB，OE平分∠COF.
①当∠C=110°时，求∠EOB的度数.
②若平行移动AB，那么∠OBC :∠OFC的值是否随之发生变化？若变化，找出变
化规律；若不变，求出这个比值.
-
科目： 来源： 题型：
查看答案和解析>>【题目】如图，已知△ABC中，AC=BC，点D、E、F分别是线段AC、BC、AD的中点，BF、ED的延长线交于点G，连接GC．
（1）求证：AB=GD；
（2）当CG=EG时，且AB=2，求CE．
-
科目： 来源： 题型：
查看答案和解析>>【题目】完成下面推理过程：
如图，已知∠1 ＝∠2，∠B ＝∠C，可推得AB∥CD．理由如下：
∵∠1 ＝∠2（已知），
且∠1 ＝∠CGD（______________________ ），
∴∠2 ＝∠CGD（等量代换）．
∴CE∥BF（___________________________）．
∴∠ ＝∠C（__________________________）．
又∵∠B ＝∠C（已知），
∴∠ ＝∠B（等量代换）．
∴AB∥CD（________________________________）.
-
科目： 来源： 题型：
查看答案和解析>>【题目】如图，△ABC中，CE和CF分别平分∠ACB和△ABC的外角∠ACD，一动点O在AC上运动，过点O作BD的平行线与∠ACB和∠ACD的角平分线分别交于点E和点F．
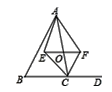
（1）求证：当点O运动到什么位置时，四边形AECF为矩形，说明理由；
（2）在第（1）题的基础上，当△ABC满足什么条件时，四边形AECF为正方形，说明理由．
-
科目： 来源： 题型：
查看答案和解析>>【题目】如图，在平面直角坐标系中，已知⊙A经过点E，B，C，O，且C（0，6）、E（﹣8，0）、O（0，0），则cos∠OBC的值为（ ）
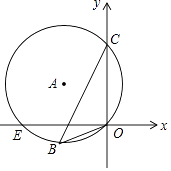
A.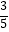
B.
C.
D.
相关试题
