【题目】如图,△ABC中,CE和CF分别平分∠ACB和△ABC的外角∠ACD,一动点O在AC上运动,过点O作BD的平行线与∠ACB和∠ACD的角平分线分别交于点E和点F.
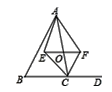
(1)求证:当点O运动到什么位置时,四边形AECF为矩形,说明理由;
(2)在第(1)题的基础上,当△ABC满足什么条件时,四边形AECF为正方形,说明理由.
参考答案:
【答案】(1)当点O运动到AC的中点位置时,四边形AECF为矩形,理由见解析;(2)当△ABC为直角三角形时,四边形AECF为正方形,理由见解析.
【解析】
(1)利用角平分线的性质以及平行线的性质得出OE=OF,即可得出结论;
(2)证出EF⊥AC,即可得出结论.
(1)证明:当点O运动到AC的中点位置时,四边形AECF为矩形;理由如下:
∵O为AC中点,
∴OA=OC,
∵EF∥BD,
∴∠CEO=∠ECB,
∵CE平分∠ACB,
∴∠BCE=∠ACE,
∴∠CEO=∠ECO,
∴OE=OC,
同理可证,OC=OF,
∴OE=OF,
∴四边形AECF为平行四边形,
又∵EF=2OE,AC=2OC,
∴EF=AC,
∴四边形AECF为矩形;
(2)解:当△ABC为直角三角形时,即∠ACB=90°时,四边形AECF为正方形;
理由如下:
∵EF∥BD,∠ACB=90°,
∴∠AOE=90°,
∴EF⊥AC,
∵四边形AECF为矩形,
∴四边形AECF为正方形.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知△ABC中,AC=BC,点D、E、F分别是线段AC、BC、AD的中点,BF、ED的延长线交于点G,连接GC.
(1)求证:AB=GD;
(2)当CG=EG时,且AB=2,求CE.

-
科目: 来源: 题型:
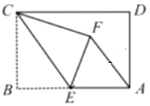
查看答案和解析>>【题目】矩形ABCD中,AB=4,BC=3,点E为AB的中点,将矩形ABCD沿CE折叠,使得点B落到点F的位置.
(1)求证:AF∥CE.
(2)求AF的长度.
-
科目: 来源: 题型:
查看答案和解析>>【题目】完成下面推理过程:
如图,已知∠1 =∠2,∠B =∠C,可推得AB∥CD.理由如下:
∵∠1 =∠2(已知),
且∠1 =∠CGD(______________________ ),
∴∠2 =∠CGD(等量代换).
∴CE∥BF(___________________________).
∴∠ =∠C(__________________________).
又∵∠B =∠C(已知),
∴∠ =∠B(等量代换).
∴AB∥CD(________________________________).

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在平面直角坐标系中,已知⊙A经过点E,B,C,O,且C(0,6)、E(﹣8,0)、O(0,0),则cos∠OBC的值为( )
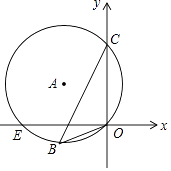
A.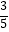
B.
C.
D.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,正方形ABCD中,AB=2
 ,O是BC边的中点,点E是正方形内一动点,OE=2,连接DE,将线段DE绕点D逆时针旋转90°得DF,连接AE,CF
,O是BC边的中点,点E是正方形内一动点,OE=2,连接DE,将线段DE绕点D逆时针旋转90°得DF,连接AE,CF
(1)如图1,求证:AE=CF;
(2)如图2,若A,E,O三点共线,求点F到直线BC的距离.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知四边形ABCD是平行四边形,对角线AC、BD交于点O,E是BC的中点,以下说法错误的是( )

A. OE=
 DC B. OA=OC C. ∠BOE=∠OBA D. ∠OBE=∠OCE
DC B. OA=OC C. ∠BOE=∠OBA D. ∠OBE=∠OCE
相关试题

