【题目】如图,△ABC中,∠B=90°,AB=6,将△ABC平移至△DEF的位置,若四边形DGCF的面积为15,且DG=4,则CF= . 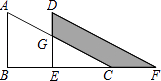
参考答案:
【答案】![]()
【解析】解:根据题意得,DE=AB=6;
设BE=CF=x,
∵CH∥DF.
∴EG=6﹣4=2;
EG:GD=EC:CF,
即 2:4=EC:x,
∴EC= ![]() x,
x,
∴EF=EC+CF= ![]() x,
x,
∴S△EFD= ![]() ×
× ![]() x×6=
x×6= ![]() x;
x;
S△ECG= ![]() ×2×
×2× ![]() x=
x= ![]() x.
x.
∴S阴影部分= ![]() x﹣
x﹣ ![]() x=15.
x=15.
解得:x= ![]() .
.
所以答案是 ![]() .
.
【考点精析】掌握平移的性质是解答本题的根本,需要知道①经过平移之后的图形与原来的图形的对应线段平行(或在同一直线上)且相等,对应角相等,图形的形状与大小都没有发生变化;②经过平移后,对应点所连的线段平行(或在同一直线上)且相等.
-
科目: 来源: 题型:
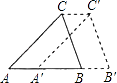
查看答案和解析>>【题目】如图,将Rt△ABC绕直角顶点C顺时针旋转90°,得到△A′B′C′,连接AA′,若∠1=27°,则∠B的度数是( )

A.84°
B.72°
C.63°
D.54° -
科目: 来源: 题型:
查看答案和解析>>【题目】指出命题“所含字母相同的单项式叫做同类项”的条件与结论,并判断其真假,若是假命题,请举出反例.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知△ABC的周长为20cm,现将△ABC沿AB方向平移2cm至△A′B′C′的位置,连接CC′,则四边形AB′C′C的周长是cm.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图1,在平面直角坐标系中,抛物线y=x2-4x-5与x轴分别交于A、B(A在B的左边),与y轴交于点C,直线AP与y轴正半轴交于点M,交抛物线于点P,直线AQ与y轴负半轴交于点N,交抛物线于点Q,且OM=ON,过P、Q作直线l
(1) 探究与猜想:
① 取点M(0,1),直接写出直线l的解析式
取点M(0,2),直接写出直线l的解析式
② 猜想:
我们猜想直线l的解析式y=kx+b中,k总为定值,定值k为__________,请取M的纵坐标为n,验证你的猜想
(2) 如图2,连接BP、BQ.若△ABP的面积等于△ABQ的面积的3倍,试求出直线l的解析式

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知△ABC各顶点的坐标分别为A(﹣2,5)B(﹣5,﹣2),C(3,3).将△ABC先向右平移4个单位长度,再向下平移3个单位长度,得到△A′B′C′.
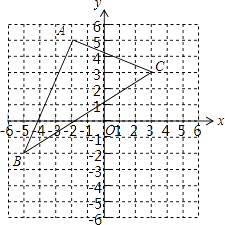
(1)在图中画出第二次平移之后的图形△A′B′C′;
(2)如果将△A′B′C′看成是由△ABC经过一次平移得到的,请指出这一平移的平移方向和平移距离. -
科目: 来源: 题型:
查看答案和解析>>【题目】在四边形ABCD中,AC与BD相交于点O,且OA=OC,OB=OD.如果再增加条件AC=BD,此四边形一定是( )
A. 正方形 B. 矩形 C. 菱形 D. 都有可能
相关试题

