【题目】如图,抛物线y=﹣ ![]() x2+bx+c与x轴交于A(﹣1,0)、B两点,与y轴交于点C(0,2),抛物线的对称轴交x轴于点D.
x2+bx+c与x轴交于A(﹣1,0)、B两点,与y轴交于点C(0,2),抛物线的对称轴交x轴于点D.
(1)求抛物线的解析式;
(2)求sin∠ABC的值;
(3)在抛物线的对称轴上是否存在点P,使△PCD是以CD为腰的等腰三角形?如果存在,直接写出点P的坐标;如果不存在,请说明理由;
(4)点E是线段BC上的一个动点,过点E作x轴的垂线与抛物线相交于点F,当点E运动到什么位置时线段EF最长?求出此时E点的坐标.
参考答案:
【答案】
(1)
解:∵抛物线y=﹣ ![]() x2+bx+c过点A(﹣1,0),C(0,2),
x2+bx+c过点A(﹣1,0),C(0,2),

![]() .
.
∴解析式为y=﹣ ![]() x2+
x2+ ![]() x+2
x+2
(2)
解:当y=0时,﹣ ![]() x2+
x2+ ![]() x+2=0解得x=﹣1(舍),x=4,
x+2=0解得x=﹣1(舍),x=4,
点B的坐标为(4,0),C(0,2),
BC= ![]() =2
=2 ![]() .
.
∴sin∠ABC=sin∠OBC= ![]() =
= ![]()
(3)
解:存在.
∵对称轴是x= ![]() ,
,
∴点D的坐标为( ![]() ,0),
,0),
∴CD= ![]() =
= ![]() .
.
PD=CD= ![]() ,得P(
,得P( ![]() ,
, ![]() )或(
)或( ![]() ,﹣
,﹣ ![]() ),
),
PC=CD= ![]() ,即P点与D点关于底边的高对称,得
,即P点与D点关于底边的高对称,得
D点的纵坐标为4,即P( ![]() ,4),
,4),
综上所述:点P的坐标为( ![]() ,
, ![]() )或(
)或( ![]() ,﹣
,﹣ ![]() ),(
),( ![]() ,4)
,4)
(4)
解:设直线BC的解析式为y=mx+n
∵B、C两点坐标分别为(4,0)、(0,2),
![]() 解得
解得  ,
,
∴直线BC的解析式为y=﹣ ![]() x+2.
x+2.
设E点坐标为(x,﹣ ![]() x+2),则F点坐标为(x,﹣﹣
x+2),则F点坐标为(x,﹣﹣ ![]() x2+
x2+ ![]() x+2),
x+2),
EF=﹣ ![]() x2+
x2+ ![]() x+2﹣(﹣
x+2﹣(﹣ ![]() x+2)
x+2)
=﹣ ![]() x2+2x
x2+2x
=﹣ ![]() (x﹣2)2+2,
(x﹣2)2+2,
当x=2时,EF最长,
∴当点E坐标为(2,1)时,线段EF最长
【解析】(1)根据待定系数法,可得函数解析式;(2)根据勾股定理,可得BC的长,根据正弦函数的定义,可得答案;(3)根据等腰三角形的定义,可得P点坐标;(4)根据平行于y轴的直线上两点间的距离是较大的纵坐标减较小的纵坐标,可得二次函数,根据二次函数的性质,可得答案.
【考点精析】掌握二次函数的图象和二次函数的性质是解答本题的根本,需要知道二次函数图像关键点:1、开口方向2、对称轴 3、顶点 4、与x轴交点 5、与y轴交点;增减性:当a>0时,对称轴左边,y随x增大而减小;对称轴右边,y随x增大而增大;当a<0时,对称轴左边,y随x增大而增大;对称轴右边,y随x增大而减小.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,矩形ABCD中,AB=8,AD=6,点E、F分别在边CD、AB上.

(1)若DE=BF,求证:四边形AFCE是平行四边形;
(2)若四边形AFCE是菱形,求菱形AFCE的周长. -
科目: 来源: 题型:
查看答案和解析>>【题目】商场进了一批家用空气净化器,成本为1200元/台.经调查发现,这种空气净化器每周的销售量y(台)与售价x(元/台)之间的关系如图所示:

(1)请写出这种空气净化器每周的销售量y与 售价x的函数关系式(不写自变量的范围);
(2)若空气净化器每周的销售利润为W(元),则当售价为多少时,可获得最大利润,此时的最大利润是多少? -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在Rt△ABC中,∠C=90°,∠ABC的平分线交AC于点D,点O是AB上一点,⊙O过B、D两点,且分别交AB、BC于点E、F.

(1)求证:AC是⊙O的切线;
(2)已知AB=10,BC=6,求⊙O的半径r. -
科目: 来源: 题型:
查看答案和解析>>【题目】某校数学兴趣小组在一次数学课外活动中,随机抽查该校10名同学参加今年初中学业水平考试的体育成绩,得到结果如下表所示:
成绩/分
36
37
38
39
40
人数/人
1
2
1
4
2
下列说法正确的是( )
A.这10名同学体育成绩的中位数为38分
B.这10名同学体育成绩的平均数为38分
C.这10名同学体育成绩的众数为39分
D.这10名同学体育成绩的方差为2 -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在Rt△ABC中,AC=5cm,BC=12cm,∠ACB=90°,把Rt△ABC所在的直线旋转一周得到一个几何体,则这个几何体的侧面积为( )

A.60πcm2
B.65πcm2
C.120πcm2
D.130πcm2 -
科目: 来源: 题型:
查看答案和解析>>【题目】二次函数y=ax2+bx+c(a、b、c是常数,且a≠0)的图象如图所示,下列结论错误的是( )
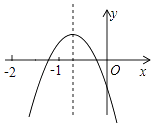
A.4ac<b2
B.abc<0
C.b+c>3a
D.a<b
相关试题

