【题目】二次函数y=ax2+bx+c(a<0)的图象与x轴的两个交点A、B的横坐标分别为﹣3、1,与y轴交于点C,下面四个结论:①16a+4b+c<0;②若P(﹣5,y1),Q(![]() ,y2)是函数图象上的两点,则y1>y2;③c=﹣3a;④若△ABC是等腰三角形,则b=﹣
,y2)是函数图象上的两点,则y1>y2;③c=﹣3a;④若△ABC是等腰三角形,则b=﹣![]() 或﹣
或﹣![]() .其中正确的有_____.(请将正确结论的序号全部填在横线上)
.其中正确的有_____.(请将正确结论的序号全部填在横线上)
参考答案:
【答案】①③④
【解析】试题解析:①∵![]()
∴抛物线开口向下,
∵图象与x轴的交点A、B的横坐标分别为-3,1,
∴当![]() 时,
时,![]() ,
,
即![]()
故①正确;
②∵图象与x轴的交点A、B的横坐标分别为-3,1,
∴抛物线的对称轴是:![]()
![]()
![]()
由对称性得:![]() 与
与![]() 是对称点,
是对称点,
∴则![]()
故②不正确;
③∵![]()
∴![]()
当x=1时,y=0,即![]()
![]()
![]() ,故③正确;
,故③正确;
④要使![]() 为等腰三角形,则必须保证
为等腰三角形,则必须保证![]() 或
或![]() 或
或![]()
当![]() 时,
时,
∵![]()
![]() 为直角三角形,
为直角三角形,
又∵OC的长即为|c|,
∴![]()
∵由抛物线与y轴的交点在y轴的正半轴上,
∴![]()
与![]() 联立组成解方程组,解得
联立组成解方程组,解得![]()
同理当![]() 时,
时,
∵![]() 为直角三角形,
为直角三角形,
又∵OC的长即为|c|,
∴![]()
∵由抛物线与y轴的交点在y轴的正半轴上,
∴![]()
与![]() 联立组成解方程组,解得
联立组成解方程组,解得![]()
同理当![]() 时,
时,
在![]() 中,
中,![]()
在![]() 中,
中,![]()
∵![]()
∴![]() ,此方程无实数解.
,此方程无实数解.
经解方程组可知有两个b值满足条件.
故④正确.
综上所述,正确的结论是①③④.
故答案为:①③④.
-
科目: 来源: 题型:
查看答案和解析>>【题目】A、B、C、D四个车站的位置如图所示:

(1)求A、D两站的距离;
(2)求C、D两站的距离;
(3)比较A、C两站的距离与B、D两站的距离,哪两站的距离更大?大多少?
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图1是一个长为
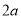 、宽为
、宽为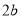 的长方形(其中
的长方形(其中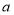 ,
,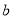 均为正数,且
均为正数,且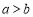 ),沿图中虚线用剪刀均匀分成四块相同小长方形,然后按图2方式拼成一个大正方形.
),沿图中虚线用剪刀均匀分成四块相同小长方形,然后按图2方式拼成一个大正方形.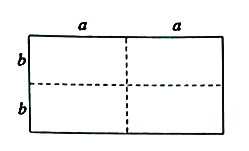
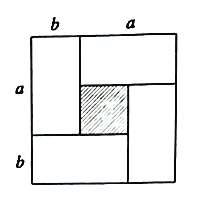
图1 图2
(1)图2中大正方形的边长为 ;小正方形(阴影部分)的边长为 .(用含
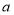 、
、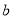 的代数式表示)
的代数式表示)(2)仔细观察图2,请你写出下列三个代数式:
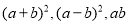 所表示的图形面积之间的相等关系,并选取适合
所表示的图形面积之间的相等关系,并选取适合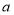 ,
,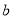 的数值加以验证.
的数值加以验证.(3)已知
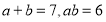 .则代数式
.则代数式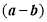 的值为 .
的值为 . -
科目: 来源: 题型:
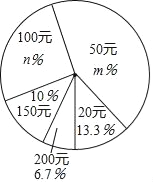
查看答案和解析>>【题目】某中学在一次爱心捐款活动中,全体同学积极踊跃捐款.现抽查了九年级(1)班全班同学捐款情况,并绘制出如下的统计表和统计图:
捐款(元)
20
50
100
150
200
人数(人)
4
12
9
3
2
求:(Ⅰ)m=_____,n=_____;
(Ⅱ)求学生捐款数目的众数、中位数和平均数;
(Ⅲ)若该校有学生2500人,估计该校学生共捐款多少元?
-
科目: 来源: 题型:
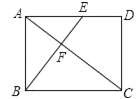
查看答案和解析>>【题目】如图,矩形ABCD中,过点B作AC的垂线交线段AD于E,垂足为F.若△CDF为等腰三角形,则
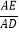 =_____.
=_____.
-
科目: 来源: 题型:
查看答案和解析>>【题目】我们在《有理数》这一章中学习过绝对值的概念:
一般的,数轴上表示数
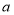 的点与原点的距离叫做数
的点与原点的距离叫做数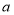 的绝对值,记作
的绝对值,记作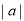 .
.实际上,数轴上表示数
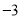 的点与原点的距离可记作
的点与原点的距离可记作 ,数轴上表示数
,数轴上表示数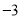 的点与表示数2的点的距离可记作
的点与表示数2的点的距离可记作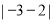 ,那么:
,那么:(1)①数轴上表示数3的点与表示数1的点的距离可记作 .
②数轴上表示数
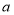 的点与表示数2的点的距离可记作 .
的点与表示数2的点的距离可记作 .③数轴上表示数
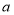 的点与表示数
的点与表示数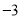 的点的距离可记作 .
的点的距离可记作 .(2)数轴上与表示数
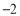 的点的距离为5的点有 个,它表示的数为 .
的点的距离为5的点有 个,它表示的数为 .(3)拓展:①当数
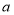 取值为 时,数轴上表示数
取值为 时,数轴上表示数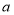 的点与表示数
的点与表示数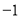 的点的距离最小.
的点的距离最小.②当整数
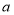 取值为 时,式子
取值为 时,式子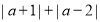 有最小值为 .
有最小值为 .③当
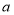 取值范围为 时,式子
取值范围为 时,式子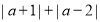 有最小值.
有最小值. -
科目: 来源: 题型:
查看答案和解析>>【题目】我们知道,任意一个正整数n都可以进行这样的分解:
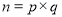 (
(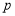 、
、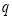 是正整数,且
是正整数,且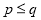 ).在n的所有这种分解中,如果
).在n的所有这种分解中,如果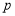 、
、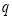 两因数之差的绝对值最小,我们就称
两因数之差的绝对值最小,我们就称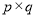 是n的最佳分解,并规定:
是n的最佳分解,并规定: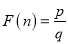 .例如12可以分解成
.例如12可以分解成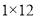 ,
,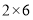 或
或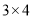 ,因为
,因为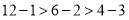 ,所以
,所以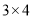 是12的最佳分解,所以
是12的最佳分解,所以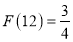 .如果一个两位正整数
.如果一个两位正整数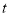 ,
,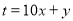 (
(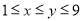 ,
,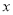 、
、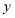 为正整数),交换其个位上的数字与十位上的数字得到的新数减去原来的两位正整数所得的差为18,那么我们称这个数
为正整数),交换其个位上的数字与十位上的数字得到的新数减去原来的两位正整数所得的差为18,那么我们称这个数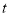 为“吉祥数”,则所有“吉祥数”中
为“吉祥数”,则所有“吉祥数”中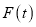 的最大值为_____________.
的最大值为_____________.
相关试题

