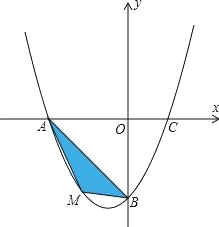
【题目】在平面直角坐标系中,已知抛物线y=![]() +bx﹣4经过A(﹣4,0),C(2,0)两点.
+bx﹣4经过A(﹣4,0),C(2,0)两点.
(1)求抛物线的解析式;
(2)若点M为第三象限内抛物线上一动点,点M的横坐标为m,△AMB的面积为S.求S关于m的函数关系式,并求出S的最大值;
(3)若点P是抛物线上的动点,点Q是直线y=﹣x上的动点,点B是抛物线与y轴交点.判断有几个位置能够使以点P、Q、B、O为顶点的四边形为平行四边形,直接写出相应的点Q的坐标.
参考答案:
【答案】(1)y=![]() +x﹣4;(2) S=
+x﹣4;(2) S=![]() ﹣4m;m=﹣2时S有最大值S=4;(3)(﹣4,4)或(
﹣4m;m=﹣2时S有最大值S=4;(3)(﹣4,4)或(![]() ,
,![]() )或(
)或(![]() ,
,![]() ).
).
【解析】
试题分析:(1)设抛物线解析式为y=![]() +bx+c,然后把点A、B、C的坐标代入函数解析式,利用待定系数法求解即可;
+bx+c,然后把点A、B、C的坐标代入函数解析式,利用待定系数法求解即可;
(2)根据图形的割补法,可得二次函数,根据抛物线的性质求出第三象限内二次函数的最值,然后即可得解;
(3)利用直线与抛物线的解析式表示出点P、Q的坐标,然后求出PQ的长度,再根据平行四边形的对边相等列出算式,然后解关于x的一元二次方程即可得解.
试题解析:(1)将A(﹣4,0),C(2,0)两点代入函数解析式,得
![]() ,
,
解得![]() ,
,
所以此函数解析式为:y=![]() +x﹣4;
+x﹣4;
(2)∵M点的横坐标为m,且点M在这条抛物线上,
∴M点的坐标为:(m,![]() +m﹣4),
+m﹣4),
∴![]() =
=![]() ×4×(
×4×(![]() +m﹣4)+
+m﹣4)+![]() ×4×(﹣m)﹣
×4×(﹣m)﹣![]() ×4×4=
×4×4=![]() ﹣4m=
﹣4m=![]() ,
,
∵﹣4<m<0,
当m=﹣2时,S有最大值为:S=﹣4+8=4,
答:S关于 m的函数关系式为S=![]() ﹣4m;m=﹣2时S有最大值S=4;
﹣4m;m=﹣2时S有最大值S=4;
(3)∵点Q是直线y=﹣x上的动点,
∴设点Q的坐标为(a,﹣a),
∵点P在抛物线上,且PQ∥y轴,
∴点P的坐标为(a,![]() +a﹣4),
+a﹣4),
∴PQ=﹣a﹣(![]() +a﹣4)=
+a﹣4)=![]() ﹣2a+4,
﹣2a+4,
又∵OB=0﹣(﹣4)=4,
以点P,Q,B,O为顶点的四边形是平行四边形,
∴|PQ|=OB,
即|![]() ﹣2a+4|=4,
﹣2a+4|=4,
①![]() ﹣2a+4=4时,整理得,
﹣2a+4=4时,整理得,![]() +4a=0,
+4a=0,
解得a=0(舍去)或a=﹣4,
﹣a=4,
所以点Q坐标为(﹣4,4),
②![]() ﹣2a+4=﹣4时,整理得,
﹣2a+4=﹣4时,整理得,![]() +4a﹣16=0,
+4a﹣16=0,
解得a=![]() ,
,
所以点Q的坐标为(![]() ,
,![]() )或(
)或(![]() ,
,![]() ).
).
综上所述,Q坐标为(﹣4,4)或(![]() ,
,![]() )或(
)或(![]() ,
,![]() )时,使点P,Q,B,O为顶点的四边形是平行四边形.
)时,使点P,Q,B,O为顶点的四边形是平行四边形.
-
科目: 来源: 题型:
查看答案和解析>>【题目】下列运算正确的是( )
A. a4a2=a8 B. a6÷a2=a3 C. (a3)2=a5 D. (2ab2)2=4a2b4
-
科目: 来源: 题型:
查看答案和解析>>【题目】“低碳环保、绿色出行”的理念得到广大群众的接受,越来越多的人喜欢选择自行车作为出行工具.小军和爸爸同时从家骑自行车去图书馆,爸爸先以150米/分的速度骑行一段时间,休息了5分钟,再以
 米/分的速度到达图书馆.小军始终以同一速度骑行,两人行驶的路程
米/分的速度到达图书馆.小军始终以同一速度骑行,两人行驶的路程 (米)与时间
(米)与时间 (分钟)的关系如图.请结合图象,解答下列问题:
(分钟)的关系如图.请结合图象,解答下列问题:(1)
 ;
; ;
; ;
;(2)若小军的速度是120米/分,求小军在图中与爸爸第二次相遇时,距图书馆的距离;
(3)在(2)的条件下,爸爸自第二次出发至到达图书馆前,何时与小军相距100米?
(4)若小军的行驶速度是
 米/分,且在图中与爸爸恰好相遇两次(不包括家、图书馆两地),请直接写出
米/分,且在图中与爸爸恰好相遇两次(不包括家、图书馆两地),请直接写出 的取值范围.
的取值范围.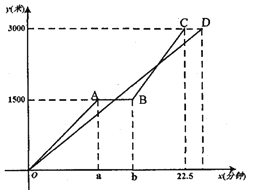
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知:(x+1)2﹣9=0,求x的值
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在平面直角坐标系中,直线l:
 与x轴、y轴分别交于点M,N,高为3的等边三角形ABC,边BC在x轴上,将此三角形沿着x轴的正方向平移,在平移过程中,得到△A1B1C1,当点B1与原点重合时,解答下列问题:
与x轴、y轴分别交于点M,N,高为3的等边三角形ABC,边BC在x轴上,将此三角形沿着x轴的正方向平移,在平移过程中,得到△A1B1C1,当点B1与原点重合时,解答下列问题:(1)求出点A1的坐标,并判断点A1是否在直线l上;
(2)求出边A1C1所在直线的解析式;
(3)在坐标平面内找一点P,使得以P、A1、C1、M为顶点的四边形是平行四边形,请直接写出P点坐标.

-
科目: 来源: 题型:
查看答案和解析>>【题目】某电器超市销售每台进价分别为200元,170元的A、B两种型号的电风扇,表中是近两周的销售情况:
销售时段
销售数量
销售收入
A种型号
B种型号
第一周
3台
5台
1800元
第二周
4台
10台
3100元
(进价、售价均保持不变,利润=销售收入﹣进货成本)
求A、B两种型号的电风扇的销售单价. -
科目: 来源: 题型:
查看答案和解析>>【题目】若一个多边形每一个内角都是150°,则这个多边形的边数是( )
A. 6B. 8C. 10D. 12
相关试题

