【题目】如图,正△ABO的边长为2,O为坐标原点,A在 ![]() 轴上,B在第二象限。△ABO沿
轴上,B在第二象限。△ABO沿 ![]() 轴正方向作无滑动的翻滚,经第一次翻滚后得△A1B1O,则翻滚3次后点B的对应点的坐标是;翻滚2017次后AB中点M经过的路径长为.
轴正方向作无滑动的翻滚,经第一次翻滚后得△A1B1O,则翻滚3次后点B的对应点的坐标是;翻滚2017次后AB中点M经过的路径长为.
参考答案:
【答案】(5, ![]() );
);![]() π
π![]()
【解析】解:(1)∵正△ABO的边长为2,第一次翻滚之后为△OA1B1,第二次翻滚之后为△B1O1A2,第三次翻滚之后为△A2B2O2,
作BD⊥x轴,
∴D为A2O2中点,
∴OD=2+2+1=5,B2D=![]() ,
,
∴B2(5, ![]() );
);
(2)∵M为AB中点
∴M经过的路径是第一次翻滚是以O为圆心,OM长为半径,圆心角为120°的扇形;第二次翻滚是以B1为圆心,B1M1长为半径,圆心角为120°的扇形;
第三次翻滚是以A2为圆心,A2M2长为半径,圆心角为120°的扇形;这样三个一循环的出现。
∵2017里面有672个3余1,
∴M经过的路径为:672×![]() +
+![]() =
=![]()
【考点精析】关于本题考查的弧长计算公式和图形的旋转,需要了解若设⊙O半径为R,n°的圆心角所对的弧长为l,则l=nπr/180;注意:在应用弧长公式进行计算时,要注意公式中n的意义.n表示1°圆心角的倍数,它是不带单位的;每一个点都绕旋转中心沿相同方向转动了相同的角度,任意一对对应点与旋转中心的连线所成的角都是旋转角,对应点到旋转中心的距离相等.旋转的方向、角度、旋转中心是它的三要素才能得出正确答案.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图是一辆小汽车与墙平行停放的平面示意图,汽车靠墙一侧与墙MN平行且距离为0.8米,已知小汽车车门宽AO为1.2米,当车门打开角度∠AOB为40°时,车门是否会碰到墙?请说明理由。(参考数据:sin40°≈0.64,cos40°≈0.77,tan40°≈0.84)

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知△ABC,AB=AC,若以点B为圆心,BC长为半径画弧,交腰AC于点E,则下列结论一定正确的是( )

A.AE=EC
B.AE=BE
C.∠EBC=∠BAC
D.∠EBC=∠ABE -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在△ABC中,AB=AC,BC=12,E为AC边的中点,线段BE的垂直平分线交边BC于点D.设BD=x,tan∠ACB=y,则( )

A.x﹣y2=3
B.2x﹣y2=9
C.3x﹣y2=15
D.4x﹣y2=21 -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,∠AOB=45°,点M,N在边OA上,OM=x,ON=x+4,点P是边OB上的点.若使点P,M,N构成等腰三角形的点P恰好有三个,则x的值是.

-
科目: 来源: 题型:
查看答案和解析>>【题目】一副含
 和
和  角的三角板
角的三角板  和
和  叠合在一起,边
叠合在一起,边  与
与  重合,
重合,  (如图1),点
(如图1),点  为边
为边 
 的中点,边
的中点,边  与
与  相交于点
相交于点 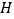 .现将三角板
.现将三角板  绕点
绕点  按顺时针方向旋转(如图2),在
按顺时针方向旋转(如图2),在 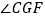 从
从  到
到  的变化过程中,点
的变化过程中,点 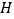 相应移动的路径长为 . (结果保留根号)
相应移动的路径长为 . (结果保留根号)
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在Rt△ABC中,∠BAC=90°,AB=15,AC=20,点D在边AC上,AD=5,DE⊥BC于点E,连结AE,则△ABE的面积等于 .

相关试题

