Question

【题目】Rt△ABC中，∠A=90°，角平分线AE、中线AD、高线AH的大小关系是（　　）
A.AH＜AE＜AD
B.AH＜AD＜AE
C.AH≤AD≤AE
D.AH≤AE≤AD

Answer 1

【答案】D
【解析】①Rt△ABC中，AB=AC；（图①）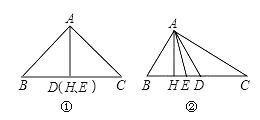

根据等腰三角形三线合一的性质知：
AD、AH、AE互相重合，此时AD=AH=AE；
②Rt△ABC中，AB≠AC；（设AC＞AB ， 如图②）
在Rt△AHE中，由于AE是斜边，故AE＞AH；
同理可证AD＞AH；
∵∠AED＞∠AHD=90°，∠ADH＜∠AHE=90°
∴∠AED＞∠ADE；
根据大角对大边知：AD＞AE；
即AD＞AE＞AH；
综上所述，角平分线AE、中线AD、高线AH的大小关系是AH≤AE≤AD；
故选D.
【考点精析】认真审题，首先需要了解解直角三角形(解直角三角形的依据：①边的关系a2+b2=c2；②角的关系：A+B=90°；③边角关系：三角函数的定义．(注意：尽量避免使用中间数据和除法))．