【题目】如图,O为直线AB上一点,OD平分∠AOC,∠DOE=90°.

(1)请你数一数,图中有 个小于平角的角;
(2)若∠AOC=50°,则∠COE的度数= ,∠BOE的度数= ;
(3)猜想:OE是否平分∠BOC?请通过计算说明你猜想的结论.
参考答案:
【答案】(1)9;(2)65°,65°;(3)OE平分∠BOC
【解析】
试题(1)根据角的表示方法结合图形的特征即可得到结果;
(2)由∠AOC=50°结合角平分线的性质可求得∠AOD、∠DOC的度数,再结合∠DOE=90°即可求得结果;
(3)设∠AOC=2α,根据角平分线的性质可得∠AOD=∠COD=![]() =α,再根据∠DOE=90°可表示出∠COE、∠BOE的度数,从而作出判断.
=α,再根据∠DOE=90°可表示出∠COE、∠BOE的度数,从而作出判断.
(1)图中有∠AOD、∠DOC、∠COE、∠BOE、∠AOC、∠DOE、∠COB、∠AOE、∠DOB共9个小于平角的角;
(2)∵∠AOC=50°,OD平分∠AOC
∴∠AOD=∠DOC=![]() =25°
=25°
∵∠DOE=90°
∴∠COE=∠DOE-∠COD=65°,∠BOE=180°-∠DOE-∠AOD=65°;
(3)结论:OE平分∠BOC.
理由:设∠AOC=2α,
∵OD平分∠AOC,∠AOC=2α,
∴∠AOD="∠COD" =![]() =α,
=α,
又∵∠DOE=90°
∴∠COE=∠DOE-∠COD=90°-α.
又∵∠BOE=180°-∠DOE-∠AOD=180°-90°-α=90°-α,
∴∠COE=∠BOE,即OE平分∠BOC.
-
科目: 来源: 题型:
查看答案和解析>>【题目】解不等式组:
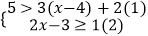 .请结合题意填空,完成本体的解法.
.请结合题意填空,完成本体的解法. 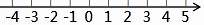
(1)解不等式(1),得;
(2)解不等式(2),得;
(3)把不等式 (1)和 (2)的解集在数轴上表示出来.
(4)原不等式的解集为 . -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,点
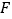 在平行四边形
在平行四边形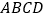 的边
的边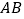 上,且
上,且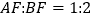 ,连接
,连接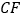 并延长,交
并延长,交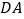 的延长线于点
的延长线于点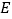 ,若
,若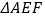 的面积为2,则平行四边形
的面积为2,则平行四边形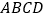 的面积为__________.
的面积为__________.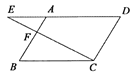
-
科目: 来源: 题型:
查看答案和解析>>【题目】植树节期间,某校倡议学生利用双休日“植树”劳动,为了解同学们劳动情况.学校随机调查了部分学生的劳动时间,并用得到的数据绘制了不完整的统计图,根据图中信息回顾下列:
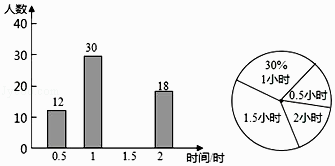
(1)通过计算,将条形图补充完整;
(2)扇形图形中“1.5小时”部分圆心角是 . -
科目: 来源: 题型:
查看答案和解析>>【题目】从⊙O外一点A引⊙O的切线AB,切点为B,连接AO并延长交⊙O于点C,点D.连接BC.
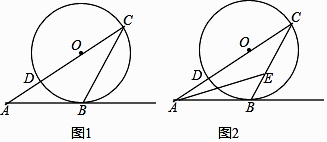
(1)如图1,若∠A=26°,求∠C的度数;
(2)如图2,若AE平分∠BAC,交BC于点E.求∠AEB的度数. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知反比例函数
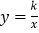 的图像经过点
的图像经过点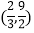 .
.(1)求k的值,并判断点
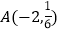 是否在该反比例函数的图像上;
是否在该反比例函数的图像上;(2)该反比例函数图像在第______象限,在每个象限内,y随x的增大而_______.
(3)当
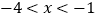 时,求y的取值范围.
时,求y的取值范围. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知一次函数
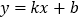 的图像与反比例函数
的图像与反比例函数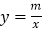 的图像交于点
的图像交于点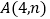 和点
和点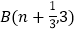 ,与
,与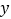 轴交于点
轴交于点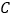 .
.(1)求反比例函数和一次函数的表达式.
(2)若在
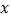 轴上有一点
轴上有一点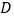 ,其横坐标是1,连接
,其横坐标是1,连接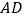 、
、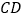 ,求
,求 的面积.
的面积.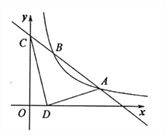
相关试题

