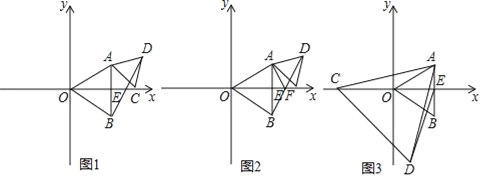
【题目】如图△AOB和△ACD是等边三角形，其中AB⊥x轴于E点．

（1）如图，若OC=5，求BD的长度；

（2）设BD交x轴于点F，求证：∠OFA=∠DFA；

（3）如图，若正△AOB的边长为4，点C为x轴上一动点，以AC为边在直线AC下方作正△ACD，连接ED，求ED的最小值.

参考答案：

【答案】（1）5；（2）见解析；（3）1.

【解析】试题分析：（1）先由等边三角形的性质得出 进而得出 即可判断出≌即可得出结论；
（2）借助（1）得出的≌，得出 进而求出 再判断出， ≌即可求出

（3）如图3中，连接DB并延长至点N，由≌（SAS），推出,推出则D点在直线BN上运动，过E作EH⊥DN于点H，当D点运动至H时，ED最小；

试题解析：(1)∵点C(5,0).

∴OC=5，

∵△AOB和△ACD是等边三角形，

∴∠OAC=∠BAD，

在△AOC和△ABD中,

∴≌，

∴BD=OC=5；

(2)∵△AOB是等边三角形，且AB⊥x轴于E点，

∴∠AOE=∠BOE=30，

由(1)知, ≌.

在△AOF和△BOF中,

∴≌.

根据平角的定义得,

∴∠OFA=∠DFA；

（3）如图3中，连接并延长至点，

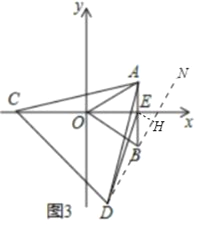
易证： ≌（SAS），

则D点在直线BN上运动

过E作于点H，当D点运动至H时，ED最小,

此时，

关闭