搜索
【题目】回顾学习函数的过程，由函数的表达式通过列表、描点、连线画出函数的图象，再利用函数图象研究函数的性质．这个过程中主要体现的数学方法是（ ）
A. 数形结合 B. 类比 C. 公理化 D. 归纳
参考答案：
【答案】A
【解析】
从函数解析式到函数图象，再利用函数图象研究函数的性质正是数形结合的数学思想的体现．
回顾学习函数的过程，由函数的表达式通过列表、描点、连线画出函数的图象，再利用函数图象研究函数的性质．这个过程中主要体现的数学方法是数形结合，
故选A．
-
科目： 来源： 题型：
查看答案和解析>>【题目】如图，在正方形网格图中建立一直角坐标系，一条圆弧经过网格点A、B、C，请在网格中进行下列操作：
（1）请在图中确定该圆弧所在圆心D点的位置，D点坐标为 ；
（2）连接AD、CD，求⊙D的半径及扇形DAC的圆心角度数；
（3）若扇形DAC是某一个圆锥的侧面展开图，求该圆锥的底面半径．
-
科目： 来源： 题型：
查看答案和解析>>【题目】凸多边形的外角和等于_____．
-
科目： 来源： 题型：
查看答案和解析>>【题目】（8分）如图，一艘轮船以15海里/时的速度，由南向北航行，在A出测得小岛P在北偏西
方向上，两小时后，轮船在B处测得小岛P在北偏西30°方向上．在小岛周围18海里内有暗礁，若轮船不改变方向仍继续向前航行，问：有无触礁的危险？说明你的理由．
-
科目： 来源： 题型：
查看答案和解析>>【题目】若y轴上的点P到x轴的距离为3，则点P的坐标是（ ）
A.（3，0）B.（0，3）
C.（3，0）或（﹣3，0）D.（0，3）或（0，﹣3）
-
科目： 来源： 题型：
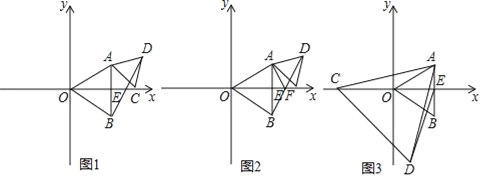
查看答案和解析>>【题目】如图△AOB和△ACD是等边三角形，其中AB⊥x轴于E点．
（1）如图，若OC=5，求BD的长度；
（2）设BD交x轴于点F，求证：∠OFA=∠DFA；
（3）如图，若正△AOB的边长为4，点C为x轴上一动点，以AC为边在直线AC下方作正△ACD，连接ED，求ED的最小值.
-
科目： 来源： 题型：
查看答案和解析>>【题目】下列计算正确的是( )
A.﹣2﹣1=﹣3B.﹣42=16C.﹣3+1=﹣4D.﹣|2|=2
相关试题
