【题目】如图,已知![]() 中,
中,![]() ,
,![]() ,点D为AB的中点.如果点P在线段BC上以2cm/s的速度由点B向C点运动,同时,点Q在线段AC上由点A向C点以4cm/s的速度运动.
,点D为AB的中点.如果点P在线段BC上以2cm/s的速度由点B向C点运动,同时,点Q在线段AC上由点A向C点以4cm/s的速度运动.
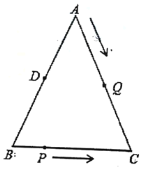
(1)若点P、Q两点分别从B、A两点同时出发,经过2秒后,![]() 与
与![]() 是否全等?请说明理由;
是否全等?请说明理由;
(2)若点P、Q两点分别从B、A两点同时出发,![]() 的周长为16cm,设运动时间为t,问:当t为何值时,是等腰三角形?
的周长为16cm,设运动时间为t,问:当t为何值时,是等腰三角形?
参考答案:
【答案】(1)△BPD与△CQP是全等.理由见解析;(2)经过1秒或2秒或1.8秒时,△CPQ是等腰三角形.
【解析】
(1)经过2秒后,PB=4m,PC=6m,AQ=8m,CQ=4m由已知可得BD=PC=6,BP=CQ=4,∠ABC=∠ACB,即据SAS可证得△BPD≌△CQP;
(2)可设点Q的运动时间为ts时△CPQ是等腰三角形,则可知PB=2tcm,PC=(10-2t)cm,AQ=4tcm,CQ=(12-4t)cm,再根据![]() 的周长为16cm,得出
的周长为16cm,得出![]() ,据(1)同理可得当CP=CQ时,当PQ=PC时,当QP=QC时,△CPQ为等腰三角形,列出方程,从而求得t的值.
,据(1)同理可得当CP=CQ时,当PQ=PC时,当QP=QC时,△CPQ为等腰三角形,列出方程,从而求得t的值.
(1)△BPD与△CQP是全等.理由如下:
当P,Q两点分别从B,A两点同时出发运动2秒时有BP=2×2=4cm,AQ=4×2=8cm,
则CP=BC-BP=10-4=6cm,CQ=AC-AQ=12-8=4cm ,
∵D是AB的中点,
∴BD=![]() AB=
AB=![]() ×12=6cm,
×12=6cm,
∴BP=CQ,BD=CP;
又∵△ABC中,AB=AC,
∴∠B=∠C ;
在△BPD和△CQP中
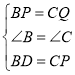
∴△BPD≌△CQP(SAS)
(2)设当P,Q两点同时出发运动t秒时,有BP=2t,AQ=4t,
∴t的取值范围为0<t≤3
则CP=10-2t,CQ=12-4t ,
∵△CPQ的周长为16cm,
∴PQ=16-(10-2t)-(12-4t)=6t-6
要使△CPQ是等腰三角形,则可分为三种情况讨论:
①当CP=CQ时,则有10-2t=12-4t,解得:t=1
②当PQ=PC时,则有6t-6=10-2t,解得:t=2;
③当QP=QC时,则有6t-6=12-4t,解得:t=1.8,
三种情况均符合t的取值范围.
综上所述,经过1秒或2秒或1.8秒时,△CPQ是等腰三角形.
-
科目: 来源: 题型:
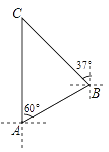
查看答案和解析>>【题目】知识改变世界,科技改变生活.导航装备的不断更新极大方便了人们的出行.如图,某校组织学生乘车到黑龙滩(用C表示)开展社会实践活动,车到达A地后,发现C地恰好在A地的正北方向,且距离A地13千米,导航显示车辆应沿北偏东60°方向行驶至B地,再沿北偏西37°方向行驶一段距离才能到达C地,求B、C两地的距离.(参考数据:sin53°≈
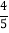 ,cos53°≈
,cos53°≈ ,tan53°≈
,tan53°≈ )
)
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知:在△ABC中,BA=BC,BD是△ABC的中线,△ABC的角平分线AE交BD于点F,过点C作AB的平行线交AE的延长线于点G
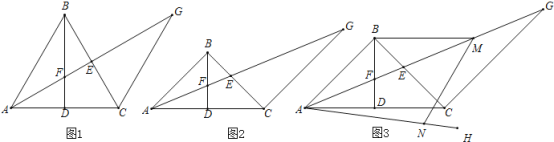
(1)如图1,若∠ABC=60°,求证:AF=
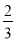 EG;
EG;(2)如图2,若∠ABC=90°,求证:AF=
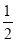 EG;
EG;(3)在(2)的条件下如图3,过点A作∠CAH=
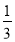 ∠FAC,过点B作BM∥AC交AG于点M,点N在AH上,连接MN、BN,若∠BMN+∠EAH=90°,
∠FAC,过点B作BM∥AC交AG于点M,点N在AH上,连接MN、BN,若∠BMN+∠EAH=90°,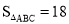 ,求BN的长.
,求BN的长. -
科目: 来源: 题型:
查看答案和解析>>【题目】阅读下列材料并解决后面的问题
材料:对数的创始人是苏格兰数学家纳皮尔(J.Npler,1550-1617年),纳皮尔发明对数是在指数书写方式之前,直到18世纪瑞士数学家欧拉(Evler,1707--1783)才发现指数与对数之间的联系,我们知道,n个相同的因数a相乘aa…,a记为an,如23=8,此时,3叫做以2为底8的对数,记为log28,即log28=3一般地若an=b(a>0且a≠1,b>0),则n叫做以a为底b的对数,记为logab,即logab=n.如34=81,则4叫做以3为底81的对数,记为log381,即log381=4.
(1)计算下列各对数的值:log24=______,log216=______,log264=______;
(2)通过观察(1)中三数log24、log216、log264之间满足的关系式是______;
(3)拓展延伸:下面这个一股性的结论成立吗?我们来证明logaM+logaN=logaMN(a>0且a≠1,M>0,N>0)
证明:设logaM=m,logaN=n,
由对数的定义得:am=M,an=N,
∴aman=am+n=MN,
∴logaMN=m+n,
又∵logaM=m,logaN=n,
∴logaM+logaN=logaMN(a>0且a≠1,M>0,N>0);
(4)仿照(3)的证明,你能证明下面的一般性结论吗?logaM-logaN=loga
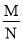 (a>0且a≠1,M>0,N>0)
(a>0且a≠1,M>0,N>0)(5)计算:log34+log39-log312的值为______.
-
科目: 来源: 题型:
查看答案和解析>>【题目】为了推进球类运动的发展,某校组织校内球类运动会,分篮球、足球、排球、羽毛球、乒乓球五项,要求每位学生必须参加一项并且只能参加一项,某班有一名学生根据自己了解的班内情况绘制了如图所示的不完整统计表和扇形统计图.

请根据图表中提供的信息,解答下列问题:
(1)图表中m=________,n=________;
(2)若该校学生共有1000人,则该校参加羽毛球活动的人数约为________人;
(3)该班参加乒乓球活动的4位同学中,有3位男同学(分别用A,B,C表示)和1位女同学(用D表示),现准备从中选出两名同学参加双打比赛,用树状图或列表法求出恰好选出一男一女的概率.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图是我县新区部分小区位置简图.设港澳城为点A,水榭花都为点B,朝阳家园为点C,滨海华庭为点D,阳光家园为点E,盛世嘉苑为点F,设每个小格的单位为1.
(1)请建立适当的平面直角坐标系,并写出六个小区的坐标;
(2)依次连接点A、C、E、B,请求出四边形ACEB的面积.

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在平面直角坐标系中,O为坐标原点,△ABC 的顶点 A (-2,0),点 B,C分别在x轴和y轴的正半轴上,∠ACB=90°,∠BAC=60°
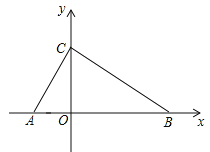
(1)求点 B 的坐标;
(2)点 P 为 AC延长线上一点,过 P 作PQ∥x轴交 BC 的延长线于点 Q ,若点 P 的横坐标为t,线段PQ的长为d,请用含t的式子表示d;
(3) 在(2)的条件下,当PA=
 d时,E是线段CQ上一点,连接OE,BP,若OE=BP,求∠APB-∠OEB的度数..
d时,E是线段CQ上一点,连接OE,BP,若OE=BP,求∠APB-∠OEB的度数..
相关试题

