【题目】如图,已知点A(3,2)和点E是正比例函数y=ax与反比例函数![]() 的图象的两个交点.
的图象的两个交点.

(1)填空:点E坐标: ;不等式![]() 的解集为 ;
的解集为 ;
(2)求正比例函数和反比例函数的关系式;
(3)P(m,n)是函数![]() 图象上的一个动点,其中0<m<3.过点P作PB⊥y轴于点B,过点A作AC⊥x轴于点C,直线PB、AC交于点D.当P为线段BD的中点时,求△POA的面积.
图象上的一个动点,其中0<m<3.过点P作PB⊥y轴于点B,过点A作AC⊥x轴于点C,直线PB、AC交于点D.当P为线段BD的中点时,求△POA的面积.
参考答案:
【答案】(1)(﹣3,﹣2),x>3或﹣3<x<0;(2)y=![]() x,y=
x,y=![]() (3)
(3)![]()
【解析】
试题分析:(1)点E的坐标是点A关于坐标原点的中心对称点,所以点E(﹣3,﹣2),观察图象即可求得不等式![]() 的解集.
的解集.
(2)把A的坐标代入解析式求出a、k即可;
(3)P为线段BD的中点求出P点的坐标值,然后用矩形的面积减去三个三角形的面积即可.
解:(1)点E坐标:(﹣3,﹣2),
不等式![]() 的解集为:x>3或﹣3<x<0.
的解集为:x>3或﹣3<x<0.
(2)把A(3,2)代入y=ax
得:2=3a,
解得:a=![]() ,
,
∴y=![]() x,
x,
代入y=![]()
得:k=6,
∴y=![]() ,
,
∴正比例函数与反比例函数的解析式分别是y=![]() x,y=
x,y=![]() .
.
(3)∵P为线段BD的中点,BD=OC=3,
∴P点的横坐标为![]() ,
,
代入y=![]() ,
,
得y=4,
∴P(![]() ,4);
,4);
S△AOP=S矩形OCDB﹣S△AOC﹣S△BOP﹣S△APD=3×4﹣![]() ×2×3﹣
×2×3﹣![]() ﹣
﹣![]() =
=![]() .
.
-
科目: 来源: 题型:
查看答案和解析>>【题目】下列命题中,是真命题的是( )
A. 对角线互相平分且相等的四边形是正方形
B. 对角线互相平分的四边形是平行四边形
C. 对角线相等的四边形是矩形
D. 对角线互相垂直的四边形是菱形
-
科目: 来源: 题型:
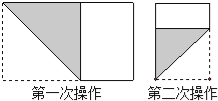
查看答案和解析>>【题目】长为30,宽为a的矩形纸片(15<a<30),如图那样折一下,剪下一个边长等于矩形宽度的正方形(称为第一次操作);再把剩下的矩形如图那样折一下,剪下一个边长等于此时矩形宽度的正方形(称为第二次操作);如此反复操作下去.若在第n次操作后,剩下的矩形为正方形,则操作终止.当n=3时,a的值为 .
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在平面直角坐标系xOy中,直线y=
 x+2与x轴交于点A,与y轴交于点C.抛物线y=ax2+bx+c的对称轴是x=﹣
x+2与x轴交于点A,与y轴交于点C.抛物线y=ax2+bx+c的对称轴是x=﹣ 且经过A、C两点,与x轴的另一交点为点B.
且经过A、C两点,与x轴的另一交点为点B.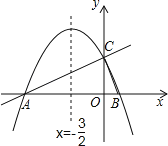
(1)①直接写出点B的坐标;②求抛物线解析式.
(2)若点P为直线AC上方的抛物线上的一点,连接PA,PC.求△PAC的面积的最大值,并求出此时点P的坐标.
(3)抛物线上是否存在点M,过点M作MN垂直x轴于点N,使得以点A、M、N为顶点的三角形与△ABC相似?若存在,求出点M的坐标;若不存在,请说明理由.
-
科目: 来源: 题型:
查看答案和解析>>【题目】某校九年级两个班各为玉树地震灾区捐款1800元.已知2班比1班人均捐款多4元,2班的人数比1班的人数少10%.请你根据上述信息,就这两个班级的“人数”或“人均捐款”提出一个用分式方程解决的问题,并写出解题过程.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在平行四边形ABCD中,对角线AC,BD相交于点O,若E,F是AC上两动点,分别从A,C两点以相同的速度向C、A运动,其速度为1cm/s.
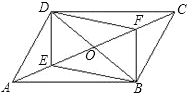
(1)当E与F不重合时,四边形DEBF是平行四边形吗?说明理由;
(2)若BD=12cm,AC=16cm,当运动时间t为何值时,以D、E、B、F为顶点的四边形是矩形?
-
科目: 来源: 题型:
查看答案和解析>>【题目】分解因式:x2﹣xy2= .
相关试题

