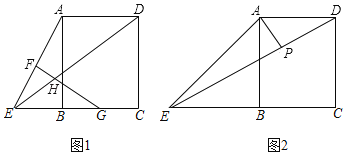
【题目】已知直线AB∥CD,将一块三角板EFG如图1所示,△EFG的边与直线AB、CD分别相交于M,N两点,∠F=90°,∠E=30°.
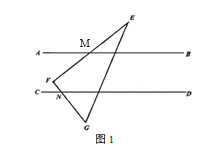
(1)求证:∠EMB+∠DNG=90°
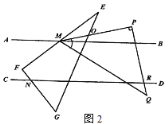
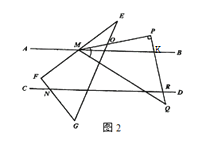
(2)将另一块三角板MPQ如图2放置,△MPQ的边PQ、PM分别与直线CD相交于点R,与△EFG的EG相交于点O,∠P=90°,∠PMQ=45°,直接写出∠PMB与∠PRD的数量关系:
参考答案:
【答案】(1)见解析(2)∠PMB+90°=∠PRD.
【解析】
(1)过点F作FH∥AB,即FH∥CD,再根据平行线的关系得到∠EMB+∠DNG=∠EFG,即可求解;
(2)根据平行线的性质及三角形的外角定理即可求解;
(1)过点F作FH∥AB,即FH∥CD,
∴∠EMB=∠EFH,∠DNG=∠HFG
∴∠EMB+∠DNG=∠EFG=90°;

(2)∠PMB+90°=∠PRD,理由如下:
设AB与PQ交于K点,
∵AB∥CD,
∴∠PRD=∠PKB,
∵∠PKB是△PMK的一个外角,
∴∠PMB+90°=∠PKB
故∠PMB+90°=∠PRD,
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知∠MAN=30°,点B在射线AM上,且 AB=6,点C在射线AN上.

(1)若△ABC是直角三角形,求AC的长;
(2)若△ABC是等腰三角形,则满足条件的C点有 个;
(3)设BC=x,当△ABC唯一确定时, 直接写出
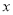 的取值范围.
的取值范围. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图1,在矩形ABCD中,E是CB延长线上一个动点,F、G分别为AE、BC的中点,FG与ED相交于点H.
(1)求证:HE=HG;
(2)如图2,当BE=AB时,过点A作AP⊥DE于点P,连接BP,求PQ与PB的数量关系,并说明理由.
-
科目: 来源: 题型:
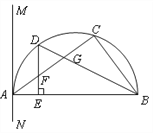
查看答案和解析>>【题目】如图,△ABC内接于半圆,AB是直径,过A作直线MN,若∠MAC=∠ABC.
(1)求证:MN是半圆的切线;
(2)设D是弧AC的中点,连结BD交AC 于G,过D作DE⊥AB于E,交AC于F.求证:FD=FG.
-
科目: 来源: 题型:
查看答案和解析>>【题目】.(1)由若干个相同的小立方体搭成的一个几何体的主视图和俯视图如图
 所示,俯视图的方格中的字母和数字表示该位置上小立方体的个数,则
所示,俯视图的方格中的字母和数字表示该位置上小立方体的个数,则 ______
______(2)如图(2),是由若干个完全相同的小正方体组成的一个几何体
①请画出这个几何体的左视图和俯视图;
 用阴影表示
用阴影表示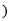
②如果在这个几何体上再添加一些相同的小正方体,并保持这个几何体的俯视图和左视图不变,那么最多可以再添加______个小正方体?
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图所示,在长方形ABCD中,AB=CD=8cm,AD=BC=6cm,点E是DC边上一点,且CE=1cm,动点P从A点出发,沿折线A-D-E以acm/s的速度向终点E运动,运动时间为t秒,已知a是方程
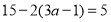 的解.
的解.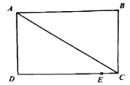
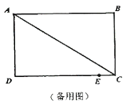
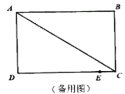
(1)求a的值;
(2)点P在运动过程中,请用t的式子表示△APC的面积;
(3)在点P运动的同时,有一动点Q从C点出发,沿折线C-D-A以1cm/s的速度向终点A运动,运动过程中,一个点停止运动时另一个点继续向终点运动,当△APC和△AQC的面积相差6平方厘米时,求t的值.
-
科目: 来源: 题型:
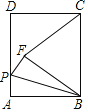
查看答案和解析>>【题目】如图,在矩形ABCD中,AB=5,BC=6,P为AD上一动点,把△ABP沿BP翻折,使点A落在点F处,连接CF,若BF=CF,则AP的长为_____.
相关试题

