【题目】若 a、b、c 为△ABC 的三边,且满足 a2+b2+c2=ab+ac+bc.点 D 是 AC边的中点,以点 D 为顶点作∠FDE=120°,角的两边分别与直线 AB 和 BC 相交于点 F 和点 E
(1)试判断△ABC 的形状,说明理由
(2)如图 1,将△ABC 图形中∠FDE=120°绕顶点 D 旋转,当两边 DF、DE 分别与边 AB 和射线BC 相交于点 F、E 时,三线段 BE、BF、AB 之间存在什么关系?证明你的结论
(3)如图 2,当角两边 DF、DE 分别与射线 AB 和射线 BC 相交两点 F、E 时,三线段 BE、BF、AB 之间存在什么关系

参考答案:
【答案】(1) △ABC为等边三角形,理由见详解;(2)3AB=2(BE+BF),证明见详解;
(3)3AB=2(BE-BF).
【解析】
(1) a2+b2+c2=ab+ac+bc,等式两边同时乘以2,可得![]() ,可得△ABC为等边三角形;
,可得△ABC为等边三角形;
(2)连接BD,过D点作DG⊥BC,延长BG至H点,使得BG=GH,可证得△BDF≌△HDE,BF=EH,由BH=BE+EH,可得BE、BF、AB 之间的关系;
(3)同理连接BD,过D点作DG⊥BC,延长BG至H点,使得BG=GH,可证得△BDF≌△HDE,BF=EH,由BH=BE-EH,可得BE、BF、AB 之间的关系;
解:(1)由a2+b2+c2=ab+ac+bc,等式两边同时乘以2,可得
2a2+2b2+2c2=2ab+2ac+2bc,可得a2+b2-2ab+ b2 +c2-2bc+ b2+c2-2ac=0
![]()
![]() ,
,![]() a=b=c,
a=b=c,
![]() △ABC为等边三角形;
△ABC为等边三角形;
(2) 如图: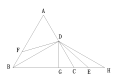
连接BD,,过D点作DG⊥BC,延长BG至H点,使得BG=GH,
易得DG为线段BH点的中垂线,![]() BD=DH
BD=DH
易得∠DBC=∠ABD=30![]() ,
,![]() ∠H=30
∠H=30![]() ,∠BDH=120
,∠BDH=120![]() ,
,
![]() ∠FDE=120°,∠BDE为∠FDE与∠BDH的公共角
∠FDE=120°,∠BDE为∠FDE与∠BDH的公共角
![]() ∠BDF=∠EDH,
∠BDF=∠EDH,
在△BDF与△EDH中,
∠ABD=∠H ;BD=DH;∠BDF=∠EDH
![]() △BDF≌△HDE
△BDF≌△HDE
![]() BF=EH,
BF=EH,
又AD=DC=![]() AC=
AC=![]() AB, ∠ACB=60
AB, ∠ACB=60![]()
![]() GC=
GC=![]() DC=
DC=![]() AB,
AB,
![]() BG= AB -
BG= AB -![]() AB=
AB=![]() AB
AB
![]() BG=GH, BH=BE+EH,
BG=GH, BH=BE+EH,
![]() 2
2![]()
![]() AB=BE+EH,
AB=BE+EH, ![]()
![]() AB= BE+BF,
AB= BE+BF,
即:3AB=2(BE+BF);
(3)如图:
同理连接BD,,过D点作DG⊥BC,延长BG至H点,使得BG=GH,
易得DG为线段BH点的中垂线,![]() BD=DH
BD=DH
可得△BDF≌△HDE
![]() BF=EH
BF=EH
可得:BH=BE-EH,![]()
![]() AB= BE-BF,
AB= BE-BF,
即3AB=2(BE-BF).
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知直线l1∥l2,且l3和l1,l2分别交于A,B两点,点P在AB上.
(1)试找出∠1,∠2,∠3之间的关系并说出理由;
(2)如果点P在A,B两点之间运动,问∠1,∠2,∠3之间的关系是否发生变化?
(3)如果点P在A,B两点外侧运动,试探究∠1,∠2,∠3之间的关系(点P和A,B不重合).

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,两直线AB,CD相交于点O,已知OE平分∠BOD,且∠AOC:∠AOD=3:7,

(1)求∠DOE的度数;
(2)若OF⊥OE,求∠COF的度数.
-
科目: 来源: 题型:
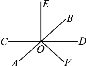
查看答案和解析>>【题目】如图所示,直线AB,CD相交于点O,OE⊥CD于点O,OD平分∠BOF,∠BOE=50°,求∠AOC、∠EOF与∠AOF的度数.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,AC⊥BC,C为垂足,CD⊥AB,D为垂足,BC=8,CD=4.8,BD=6.4,AD=3.6,AC= 6,那么点C到AB的距离是_______,点A到BC的距离是________,点B到CD 的距离是_____,A、B两点的距离是_________.
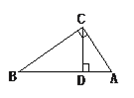
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图:二次函数y=ax2+bx+c的图象所示,下列结论中:①abc>0;②2a+b=0;③当m≠1时,a+b>am2+bm;④a﹣b+c>0;⑤若ax12+bx1=ax22+bx2 , 且x1≠x2 , 则x1+x2=2,正确的个数为( )
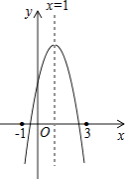
A.1个
B.2个
C.3个
D.4个 -
科目: 来源: 题型:
查看答案和解析>>【题目】为了解当地气温变化情况,某研究小组记录了寒假期间连续6天的最高气温,结果如下(单位:℃):﹣6,﹣3,x,2,﹣1,3,若这组数据的中位数是﹣1,在下列结论中:①方差是8;②极差是9;③众数是﹣1;④平均数是﹣1,其中正确的序号是 .
相关试题

