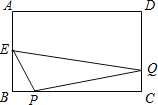
【题目】如图,在矩形ABCD中,AB=4,BC=6,E为AB中点,动点P从点B开始沿BC方向运动到点C停止,动点Q从点C开始沿CD﹣DA方向运动,与点P同时出发,同时停止.这两点的运动速度均为每秒1个单位.若设他们的运动时间为x(秒),△EPQ的面积为y,则y与x之间的函数关系的图象大致是( )
A.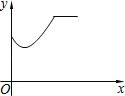 B.
B.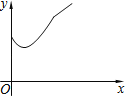 C.
C.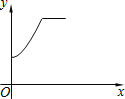 D.
D.
参考答案:
【答案】A
【解析】
试题分析:先求出点P在BC上运动是时间为6秒,点Q在CD上运动是时间为4秒,再根据中点的定义可得AE=BE=![]() AB,然后分①点Q在CD上时,表示出BP、CP、CQ,再根据△EPQ的面积为y=S梯形BCQE﹣S△BPE﹣S△PCQ,列式整理即可得解;②点Q在AD上时,表示出BP、AQ,再根据△EPQ的面积为y=S梯形ABPQ﹣S△BPE﹣S△AEQ,列式整理即可得解,再根据函数解析式确定出函数图象即可.
AB,然后分①点Q在CD上时,表示出BP、CP、CQ,再根据△EPQ的面积为y=S梯形BCQE﹣S△BPE﹣S△PCQ,列式整理即可得解;②点Q在AD上时,表示出BP、AQ,再根据△EPQ的面积为y=S梯形ABPQ﹣S△BPE﹣S△AEQ,列式整理即可得解,再根据函数解析式确定出函数图象即可.
解:∵点P、Q的速度均为每秒1个单位,
∴点P在BC上运动的时间为6÷1=6秒,
点Q在CD上运动的时间为4÷1=4秒,
∵E为AB中点,
∴AE=BE=![]() AB=
AB=![]() ×4=2,
×4=2,
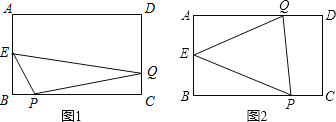
①如图1,点Q在CD上时,0≤x≤4,
BP=x,CP=6﹣x,CQ=x,
△EPQ的面积为y=S梯形BCQE﹣S△BPE﹣S△PCQ,
=![]() (2+x)×6﹣
(2+x)×6﹣![]() 2x﹣
2x﹣![]() (6﹣x)x,
(6﹣x)x,
=![]() x2﹣x+6,
x2﹣x+6,
=![]() (x﹣1)2+
(x﹣1)2+![]() ;
;
②如图2,点Q在AD上时,4<x≤6,
BP=x,AQ=6+4﹣x=10﹣x,
△EPQ的面积为y=S梯形ABPQ﹣S△BPE﹣S△AEQ,
=![]() (x+10﹣x)×4﹣
(x+10﹣x)×4﹣![]() 2x﹣
2x﹣![]() (10﹣x)2,
(10﹣x)2,
=10,
综上所述,y=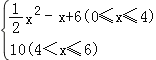 ,
,
函数图象为对称轴为直线x=1的抛物线的一部分加一条线段,
纵观各选项,只有A选项符合.
故选A.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在平行四边形ABCD中,以点A为圆心,AB长为半径画弧交AD于点F,再分别以点B、F为圆心,大于
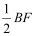 长为半径画弧,两弧交于一点P,连接AP并延长交BC于点E,连接EF.
长为半径画弧,两弧交于一点P,连接AP并延长交BC于点E,连接EF.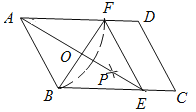
(1)四边形ABEF是_______;(选填矩形、菱形、正方形、无法确定)(直接填写结果)
(2)AE,BF相交于点O,若四边形ABEF的周长为40,BF=10,则AE的长为________,∠ABC=________°.(直接填写结果)
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知线段AB=12,CD=6,线段CD在直线AB上运动(A在B的左侧,C在D的左侧).
(1)当D点与B点重合时,AC=_________;
(2)点P是线段AB延长线上任意一点,在(1)的条件下,求PA+PB–2PC的值;
(3)M、N分别是AC、BD的中点,当BC=4时,求MN的长.

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在平面直角坐标系xOy中,分别平行x、y轴的两直线a、b相交于点A(3,4).连接OA,
线段OA长______; (2)若在直线a上存在点P,使△AOP是以OA为腰的等腰三角形.那么所有满足条件的点P的坐标是________________.

-
科目: 来源: 题型:
查看答案和解析>>【题目】我市某校开展了以“梦想中国”为主题的摄影大赛,要求参赛学生每人交一件作品.现将
从中挑选的50件参赛作品的成绩(单位:分)统计如下:
等级
成绩(用m表示)
频数
频率
A
90≤ m ≤100
x
0.08
B
80≤ m <90
34
y
C
m <80
12
0.24
合计
50
1
请根据上表提供的信息,解答下列问题:
(1)表中
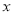 的值为_____________,
的值为_____________,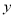 的值为______________;(直接填写结果)
的值为______________;(直接填写结果)(2)将本次参赛作品获得A等级的学生依次用A1、A2、A3……表示.现该校决定从本次参赛作品获得A等级的学生中,随机抽取两名学生谈谈他们的参赛体会,则恰好抽到学生A1和A2的概率为____________.(直接填写结果)
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,平行四边形ABCD中,BD⊥AD,∠A=45°,E、F分别是AB、CD上的点,且BE=DF,连接EF交BD于O.
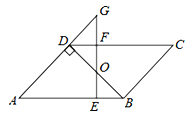
(1)求证:BO=DO;
(2)若EF⊥AB,延长EF交AD的延长线于G,当FG=1时,求AE的长.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在Rt△ABC中,∠ACB=90°,AC=5cm,∠BAC=60°,动点M从点B出发,在BA边上以每秒2cm的速度向点A匀速运动,同时动点N从点C出发,在CB边上以每秒
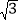 cm的速度向点B匀速运动,设运动时间为t秒(0≤t≤5),连接MN.
cm的速度向点B匀速运动,设运动时间为t秒(0≤t≤5),连接MN.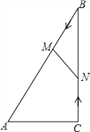
(1)若BM=BN,求t的值;
(2)若△MBN与△ABC相似,求t的值;
(3)当t为何值时,四边形ACNM的面积最小?并求出最小值.
相关试题

